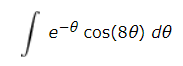Me and a friend can't solve this one problem, please help.
- Thread starter afresz
- Start date
Hey, I'm the friend. So far we have:
1/8sin(8x)e^-x + 1/64cos(8x)(-e^-x) + 1/64 int. cos(8x)e^-x
Apologies for formatting; I'm new to this. Treat x as theta. This was after taking u=e^-x, and dv=cos(8x)
cos(8x)(-e^-x) - int. -e^-x (-8sin(8x))dx
is what he's gotten so far, replacing theta with x
- Joined
- Nov 24, 2012
- Messages
- 3,021
Okay, I would let:
[MATH]I=\int e^{-\theta}\cos(8\theta)\,d\theta[/MATH]
where
[MATH]u=\cos(8\theta)\implies du=-8\sin(8\theta)\,d\theta[/MATH]
[MATH]dv=e^{-\theta}\,d\theta\implies v=-e^{-\theta}[/MATH]
And so we have:
[MATH]I=-e^{-\theta}\cos(8\theta)+8\int e^{-\theta}\sin(8\theta)\,d\theta[/MATH]
This is equivalent to what your friend has. So, so use IBP in the remaining integral on the RHS. What do you get?
[MATH]I=\int e^{-\theta}\cos(8\theta)\,d\theta[/MATH]
where
[MATH]u=\cos(8\theta)\implies du=-8\sin(8\theta)\,d\theta[/MATH]
[MATH]dv=e^{-\theta}\,d\theta\implies v=-e^{-\theta}[/MATH]
And so we have:
[MATH]I=-e^{-\theta}\cos(8\theta)+8\int e^{-\theta}\sin(8\theta)\,d\theta[/MATH]
This is equivalent to what your friend has. So, so use IBP in the remaining integral on the RHS. What do you get?