Yo!
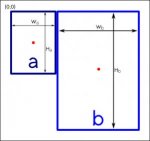
So, the issue is basically to get from Image 1 to Image 2.
Original setup:

The red dots are the mid-points (x & y).
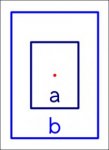
Now. How much do I need to compensate (relatively) on B's origin x & y values to match up B's midpoint with A's midpoint and end up with this:

You can assume a standard Cartesian plane, so negative values are fine. The most important thing is that A will never move. B must move relative to A to make sure the midpoints match up exactly.
Can anyone help?
So, the issue is basically to get from Image 1 to Image 2.
Original setup:
The red dots are the mid-points (x & y).
Now. How much do I need to compensate (relatively) on B's origin x & y values to match up B's midpoint with A's midpoint and end up with this:
You can assume a standard Cartesian plane, so negative values are fine. The most important thing is that A will never move. B must move relative to A to make sure the midpoints match up exactly.
Can anyone help?