You are using an out of date browser. It may not display this or other websites correctly.
You should upgrade or use an alternative browser.
You should upgrade or use an alternative browser.
Need help to solve a geometry problem
- Thread starter shan86
- Start date
Harry_the_cat
Elite Member
- Joined
- Mar 16, 2016
- Messages
- 3,784
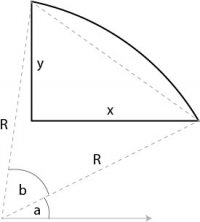
If the angle between side x and side y is a right angle, you could use Pythagoras' theorem to find the length of the other dotted line. Then use some basic trig to find angle b.
mmm4444bot
Super Moderator
- Joined
- Oct 6, 2005
- Messages
- 10,962
Posting Guidelines (Summary)
Welcome to our tutoring boards! :) This page summarizes main points from our posting guidelines. As our name implies, we provide math help (primarily to students with homework). We do not generally post immediate answers or step-by-step solutions. We don't do your homework. We prefer to help...
www.freemathhelp.com
Hi, thanks for the reply. Yes, x and y is a right angle. And I can find the length of the hypotenuse. But then, I don't know how to find those angles. Please help meIf the angle between side x and side y is a right angle, you could use Pythagoras' theorem to find the length of the other dotted line. Then use some basic trig to find angle b.
Hi, thanks for the reply. Yes, x is parallel to the arrow at the bottom. And x and y forms a right angle. Please let me know how to find those angles.We need to know is the line marked x parallel to the line with the arrow at the bottom, and is the line marked y perpendicular to the line marked x.
Ok, sorry I missed that. I'm a software developer and I need to work on a project that involves 2D shapes. This is stripped down version of the problem that I'm facing right now. Basically, I need to draw this shape, based on the X, Y and R, which are user inputs.Posting Guidelines (Summary)
Welcome to our tutoring boards! :) This page summarizes main points from our posting guidelines. As our name implies, we provide math help (primarily to students with homework). We do not generally post immediate answers or step-by-step solutions. We don't do your homework. We prefer to help...www.freemathhelp.com
Basically you need to find the co-ordinates of the corner of the shape (at the right angle).
Altering your notation slightly:
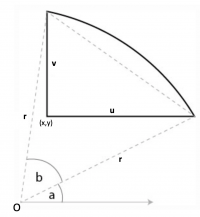
you simply need to solve the simultaneous quadratic equations in x and y:
1. [imath](x+u)^2+y^2=r^2[/imath]
2. [imath]x^2+(y+v)^2=r^2[/imath]
This yields a solution [imath]x=\dfrac{-u+\sqrt{u^2-4\alpha}}{2}, y=\sqrt{r^2-(x+u)^2}[/imath]
where [imath]\alpha=\dfrac{u^2+v^2}{4}-\dfrac{v^2r^2}{u^2+v^2}[/imath]
(Depending on whether u and/or v are less than r, there may be a corresponding solution in each of the 4 quadrants, in 2 quadrants, in only 1 quadrant or no solution if u, v are 'too large' relative to r).
Altering your notation slightly:

you simply need to solve the simultaneous quadratic equations in x and y:
1. [imath](x+u)^2+y^2=r^2[/imath]
2. [imath]x^2+(y+v)^2=r^2[/imath]
This yields a solution [imath]x=\dfrac{-u+\sqrt{u^2-4\alpha}}{2}, y=\sqrt{r^2-(x+u)^2}[/imath]
where [imath]\alpha=\dfrac{u^2+v^2}{4}-\dfrac{v^2r^2}{u^2+v^2}[/imath]
(Depending on whether u and/or v are less than r, there may be a corresponding solution in each of the 4 quadrants, in 2 quadrants, in only 1 quadrant or no solution if u, v are 'too large' relative to r).
Dr.Peterson
Elite Member
- Joined
- Nov 12, 2017
- Messages
- 16,852
If you need to find the angles rather than coordinates, I would do this:
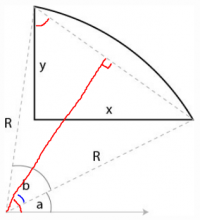
Using the right triangle with legs x and y, find the diagonal, and also find the angle marked in red. This is congruent to the red angle at the origin, because the sides of the angles are perpendicular.
Then using the right triangle with the red line as a leg, find the angle marked in blue. From those two angles, you can find a and b.

Using the right triangle with legs x and y, find the diagonal, and also find the angle marked in red. This is congruent to the red angle at the origin, because the sides of the angles are perpendicular.
Then using the right triangle with the red line as a leg, find the angle marked in blue. From those two angles, you can find a and b.
Thanks @lex, for the detailed explanation. This helps a lot.Basically you need to find the co-ordinates of the corner of the shape (at the right angle).
Altering your notation slightly:
View attachment 28857
you simply need to solve the simultaneous quadratic equations in x and y:
1. [imath](x+u)^2+y^2=r^2[/imath]
2. [imath]x^2+(y+v)^2=r^2[/imath]
This yields a solution [imath]x=\dfrac{-u+\sqrt{u^2-4\alpha}}{2}, y=\sqrt{r^2-(x+u)^2}[/imath]
where [imath]\alpha=\dfrac{u^2+v^2}{4}-\dfrac{v^2r^2}{u^2+v^2}[/imath]
(Depending on whether u and/or v are less than r, there may be a corresponding solution in each of the 4 quadrants, in 2 quadrants, in only 1 quadrant or no solution if u, v are 'too large' relative to r).
Thanks @Dr. Peterson, Your solution is the easiest. I think I can go with this. I'll update the result. Thanks again.If you need to find the angles rather than coordinates, I would do this:
View attachment 28858
Using the right triangle with legs x and y, find the diagonal, and also find the angle marked in red. This is congruent to the red angle at the origin, because the sides of the angles are perpendicular.
Then using the right triangle with the red line as a leg, find the angle marked in blue. From those two angles, you can find a and b.
If anyone interested, this is how I implemented it in c/c++. Thanks everyone.
C:
double l = ::sqrt(x*x + y*y) / 2.0;
double a1 = ::atan2(x, y);
double a2 = ::asin(l / r);
double a3 = a1 - a2;
_ASSERT(a1 > a2);
double b = a2 * 2;
double a = a1 - a2;