Normal Vector to a Plane Problem

[Starblazer]

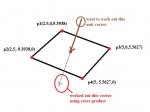
The problem requires that a find the unit vector normal to the plane and "slide it back" so it is pointing into the plane (see picture)
I have so far
\(\displaystyle \begin{array}{l}
p1 < 2.5,0,9.3938 > \\
p2 < 2.5, - 9.3938,0 > \\
p3 < 5,0,5.5627 > \\
p4 < 5. - 5.5627,0 > \\
v1 = p1 - p3\\
v2 = p4 - p3
\end{array}\)
Workout Cross Product
\(\displaystyle v1 \times v2 = - 21.3113i + 13.9069j - 13.9069k = vcp\)
Then make it a unit vector
\(\displaystyle \begin{array}{l}
\left| {vcp} \right| = \sqrt {{{\left( { - 21.3113} \right)}^2} + {{\left( {13.9069} \right)}^2} + {{\left( { - 13.9069} \right)}^2}} = 28.99957\\
\mathop v\limits^\^ = < \frac{{ - 21.3113}}{{28.99957}},\frac{{13.9069}}{{28.99957}},\frac{{ - 13.9069}}{{28.99957}} >
\end{array}\)
Find Centre of Plane
\(\displaystyle \begin{array}{l}
x = (2.5 + 2.5 + 5 + 5)/4 = 3.75\\
y = (0 - 9.3938 + 0 - 5.5627)/4 = - 3.73913\\
z = (9.3938 + 0 + 5.5627 + 0)/4 = 3.739125
\end{array}\)
So I have the dashed vector (see diagram)
Now I need brown vector
The Method suggested was to use
\(\displaystyle \sqrt {{{\left( {{x_b} - 3.75} \right)}^2} + {{\left( {{y_b} - - 3.73913} \right)}^2} + {{\left( {{z_b} - 3.739125} \right)}^2}} = 1\)
where the numbers are the centre point and xb,yb,zb are the tail of the vector

 

[HallsofIvy]

Do you want a vector or a point? If a vector then where it is is irrelevant. The cross product of two vectors in the plane is normal to the plane and dividing by its length gives the unit vector normal to the plane. the "two" vectors you show in your picture are two different representations of the same vector.

 

[Starblazer]

Thanks for the reply. I need this for a MATLAB computer program. I think I want a point. I need the head of the vector to be touching the surface, as in the picture.

I want to call quiver3 In Matlab to do that I need.

quiver3(x,y,z,u,v,w) plots vectors with components (u,v,w) at the points (x,y,z).

At the moment it is drawing the grey dashed vector. I am passing the funtion
quiver3(centre_of_plane_point_x,centre_of_plane_point_y,centre_of_plane_point_z,cross_product_unit_vect_x, cross_product_unit_vect_y,cross_product_unit_vect_z );

 

[Bob Brown MSEE]

v1 = p1 - p3
v2 = p4 - p3

Notice that if you add some number n1 to all x-vals
Notice that if you add some number n2 to all y-vals
You will get the same v1 and v2

Conclusion: All sheets this size and parallel to this sheet, will yield the same cross-product.

 

[Starblazer]

quiver3 takes 3 components of vector u,v,w which are correct, but instead of giving it the x,y,z of the panel center (that will make the tail of the vector at the center point), you need to give it x-u,y-v,z-w (that will "slide" the vector backward so its head is now at the panel center)

quiver3(centre(1)-vectUnit(1),centre(2)-vectUnit(2),centre(3)-vectUnit(3), vectUnit(1),vectUnit(2),vectUnit(3) );
with figures
\(\displaystyle quiver3(3.75 - \frac{{ - 21.3113}}{{28.99957}}, - 3.73913 - \frac{{13.9069}}{{28.99957}},3.739125 - \frac{{ - 13.9069}}{{28.99957}},\frac{{ - 21.3113}}{{28.99957}},\frac{{13.9069}}{{28.99957}},\frac{{ - 13.9069}}{{28.99957}})\)