Help!
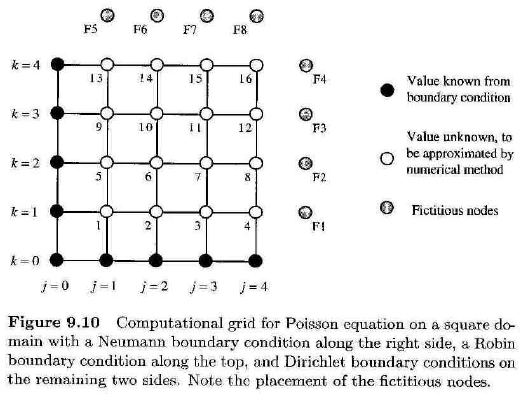
I need to know how to approximate this Laplace equation:
\(\displaystyle (\partial^2 u)/(\partial x^2) + (\partial^2 u)/(\partial y^2) = 0 \;\; \text{with boundary conditions:}\)
\(\displaystyle u(x,0) = 0\)
\(\displaystyle \dfrac{\partial u(x,1)}{\partial y}+\dfrac{2u(x,1)}{(1+x^2)+1} = \dfrac{1}{(1+x^2)+1}\)
\(\displaystyle u(0,y) = \dfrac{y}{1+y^2}\)
\(\displaystyle \dfrac{\partial u(1,y)}{\partial x} = - \dfrac{4y}{(4+y^2)^2}\)
I would REALLY appreciate some help.
I need to know how to approximate this Laplace equation:
\(\displaystyle (\partial^2 u)/(\partial x^2) + (\partial^2 u)/(\partial y^2) = 0 \;\; \text{with boundary conditions:}\)
\(\displaystyle u(x,0) = 0\)
\(\displaystyle \dfrac{\partial u(x,1)}{\partial y}+\dfrac{2u(x,1)}{(1+x^2)+1} = \dfrac{1}{(1+x^2)+1}\)
\(\displaystyle u(0,y) = \dfrac{y}{1+y^2}\)
\(\displaystyle \dfrac{\partial u(1,y)}{\partial x} = - \dfrac{4y}{(4+y^2)^2}\)
I would REALLY appreciate some help.
Last edited by a moderator: