I do not know how to solve this problem:
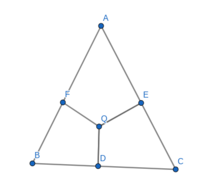
In an isosceles triangle with sides 5 cm, 5 cm, 8 cm, a point Q inside the triangle is chosen. Perpendiculars are drawn from it, which divide the triangle into 3 similar triangles. Find the lengths of the perpendiculars; the distance from Q to the sides
In an isosceles triangle with sides 5 cm, 5 cm, 8 cm, a point Q inside the triangle is chosen. Perpendiculars are drawn from it, which divide the triangle into 3 similar triangles. Find the lengths of the perpendiculars; the distance from Q to the sides