Pls help ASAP how to find the distance from a vertex of a pentagon to its center knowing each side = 1

T

thxeveryone

New member
Joined
May 27, 2024
Messages
5
I found https://www.pulsus.com/scholarly-ar...sis-of-regular-pentagonal-right-antiprism.pdf:
1716819277209.png
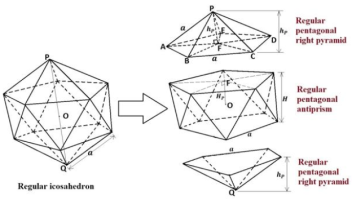
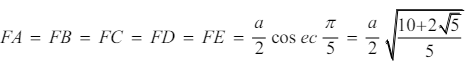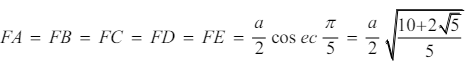1716819324242.png for the pentagonal pyramid but I'm not sure if cos ec means csc. I understand why FA = FB = FC = FD = FE but I have no idea where a/2(cos ec pi/5) came from. I am not good with trig or calc, so pls try to explain it as simple as you can... Or can you guys just explain how to find BF or FC using the fact that triangle BFC is isosceles and BC = 1?

I'm guessing pi is used since the pentagonal base can be inscribed inside a circle but I still don't understand if this is right then why don't we use 2pi like for circumference).

Pls, all help would be very much appreciated... this is due soon...
 
Last edited:
So like I thought about the method I mentioned but it doesn't line up with the formula. Angle BFC should be 360/5 = 72, and since BF = BC, (180-72)/2 = angle FBC = angle FCB = 36. By the law of sines BF and BC should equal (sin36)/((sin72)/a) = (sin36)/((sin72)/1) = (sin36)/(sin72) = 0.618... but this isn't equal to (1/2)(rad (10+2rad5)/5) = 0.85...

With a little bit trial and error I got that the formula is (a/2)(1/(sin pi/5))= (a/2)(1/(sin36)) but I still don't understand why my previous method with the law of sines is incorrect.
 
Last edited:
You must log in or register to reply here.
Top