A class of 30 students has 16 boys and 14 girls. How many groups of 8 students can be formed where
(a) the eldest boy is included in the group?
(b) the eldest boy is excluded from the group?
(c) the eldest boy is excluded if the eldest girl is included (i.e. they can't both be on the committee)
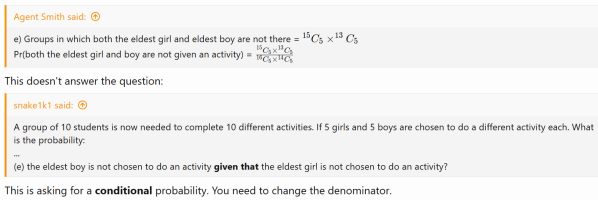
A group of 10 students is now needed to complete 10 different activities. If 5 girls and 5 boys are chosen to do a different activity each. What is the probability:
(d) the eldest boy is chosen to do an activity?
(e) the eldest boy is not chosen to do an activity given that the eldest girl is not chosen to do an activity?
The class of 30 students is now broken into 2 groups, each containing 15 students.
(f) How many ways can the 2 groups be formed
(g) What is the probability that there are 8 boys and 7 girls in each group?
(a) the eldest boy is included in the group?
(b) the eldest boy is excluded from the group?
(c) the eldest boy is excluded if the eldest girl is included (i.e. they can't both be on the committee)
A group of 10 students is now needed to complete 10 different activities. If 5 girls and 5 boys are chosen to do a different activity each. What is the probability:
(d) the eldest boy is chosen to do an activity?
(e) the eldest boy is not chosen to do an activity given that the eldest girl is not chosen to do an activity?
The class of 30 students is now broken into 2 groups, each containing 15 students.
(f) How many ways can the 2 groups be formed
(g) What is the probability that there are 8 boys and 7 girls in each group?