You are using an out of date browser. It may not display this or other websites correctly.
You should upgrade or use an alternative browser.
You should upgrade or use an alternative browser.
Problem with Sine Law: Find the length of the inner bisector of the corner at the top A.
- Thread starter Aysun
- Start date
This is the image.
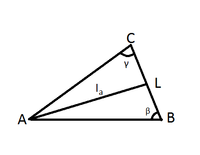
And I think this should be the solution:
\(\displaystyle \angle\)CAB=180 \(\displaystyle ^\circ\) - (\(\displaystyle \beta\) + \(\displaystyle \gamma\))
\(\displaystyle \Rightarrow\) \(\displaystyle \angle\)CAL=\(\displaystyle \angle\)LAB=\(\displaystyle \frac{180 ^\circ - (\beta+\gamma)}{2}\)
here we use the sines law:
\(\displaystyle \frac{AL}{sin\gamma}\)=\(\displaystyle \frac{CL}{\frac{sin180 ^\circ - (\beta+\gamma))}{2}}\)
\(\displaystyle \Rightarrow\) \(\displaystyle \frac{AL}{sin\gamma}\)=\(\displaystyle \frac{2CL}{sin( \beta+\gamma)}\)
\(\displaystyle \Rightarrow\) AL=\(\displaystyle \frac{2CL.sin \gamma}{sin(\beta+\gamma)}\)
And if I use the sines law for the triangle ALB:
AL=\(\displaystyle \frac{2LB.sin\beta}{sin(\beta+\gamma)} \)
Is it right ? I'm sorry if I have made any mistakes.My English is not that good.

And I think this should be the solution:
\(\displaystyle \angle\)CAB=180 \(\displaystyle ^\circ\) - (\(\displaystyle \beta\) + \(\displaystyle \gamma\))
\(\displaystyle \Rightarrow\) \(\displaystyle \angle\)CAL=\(\displaystyle \angle\)LAB=\(\displaystyle \frac{180 ^\circ - (\beta+\gamma)}{2}\)
here we use the sines law:
\(\displaystyle \frac{AL}{sin\gamma}\)=\(\displaystyle \frac{CL}{\frac{sin180 ^\circ - (\beta+\gamma))}{2}}\)
\(\displaystyle \Rightarrow\) \(\displaystyle \frac{AL}{sin\gamma}\)=\(\displaystyle \frac{2CL}{sin( \beta+\gamma)}\)
\(\displaystyle \Rightarrow\) AL=\(\displaystyle \frac{2CL.sin \gamma}{sin(\beta+\gamma)}\)
And if I use the sines law for the triangle ALB:
AL=\(\displaystyle \frac{2LB.sin\beta}{sin(\beta+\gamma)} \)
Is it right ? I'm sorry if I have made any mistakes.My English is not that good.
