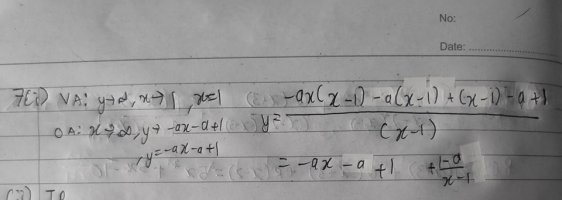Proving the x-coordinates of the turning points of a graph is positive
- Thread starter Antroph1c
- Start date
D
Deleted member 4993
Guest
What are the mathematical characteristics of turning point ?
Hello, If I'm not mistaken, to find the coordinates of the turning points, the first differential of the y in the equation has to be equal to 0?( From there the x-coordinates of the turning points can be found).
Besides that, I'm fairly certain that my oblique asymptote is correct, i forgot the name of the method i used to find the OA, however I was taught this in my class.
This question was taken from a CIE further mathematics(9231) a levels past year paper from 2004, and I found the answer online, (I've attached the file below),I just don't fully understand the way the marking scheme explained how to prove it.
Sorry for the long paragraphs, do let me know if i need to clarify anything else. Thank you very much in advance ^_^
Besides that, I'm fairly certain that my oblique asymptote is correct, i forgot the name of the method i used to find the OA, however I was taught this in my class.
This question was taken from a CIE further mathematics(9231) a levels past year paper from 2004, and I found the answer online, (I've attached the file below),I just don't fully understand the way the marking scheme explained how to prove it.
Sorry for the long paragraphs, do let me know if i need to clarify anything else. Thank you very much in advance ^_^
Last edited:
@Antroph1c
You are correct concerning the turning points. What do you not understand about their solution?
You can differentiate [imath]y=-ax+(1-a)+(1-a)(x-1)^{-1}[/imath] and set it equal to 0.
This finds stationary values, but from the question I think you can then assume that they are actually turning points.
You simply now have to show that they are real values (involving the square root of a non-negative number, in fact they are [imath]1\pm \sqrt{\tfrac{a-1}{a}}[/imath])
and that they are both positive (i.e. that [imath]\sqrt{\tfrac{a-1}{a}}<1[/imath])
You are correct concerning the turning points. What do you not understand about their solution?
You can differentiate [imath]y=-ax+(1-a)+(1-a)(x-1)^{-1}[/imath] and set it equal to 0.
This finds stationary values, but from the question I think you can then assume that they are actually turning points.
You simply now have to show that they are real values (involving the square root of a non-negative number, in fact they are [imath]1\pm \sqrt{\tfrac{a-1}{a}}[/imath])
and that they are both positive (i.e. that [imath]\sqrt{\tfrac{a-1}{a}}<1[/imath])