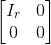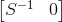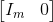\(\displaystyle A \in M_{m \times n}\) , \(\displaystyle S \in M_{m \times m} \) and \(\displaystyle T \in M_{n \times n} \).
\(\displaystyle A\) has rank [MATH] r(A) = r[/MATH].
Prove that if both [MATH]S[/MATH] and [MATH]T[/MATH] are invertible such that [MATH] SAT_{m \times n} =[/MATH]
then if [MATH]r=m[/MATH] or [MATH]r=n[/MATH] there aren't either null lines (in the previous case) or null columns (in the later case) ?
For starters,
If [MATH]r = m[/MATH], then I don't understand the need for two null matrices in the bottom rows because [MATH]I_{r}[/MATH] occupies all rows. The same goes for [MATH]r = n[/MATH] but for columns...
After this point, I don't really know how to approach this problem and need some guidance.
My first thought was to try and see what happens if [MATH]AT =[/MATH]
. In that case [MATH]SAT =[/MATH]
but it doesn't necessarily mean [MATH]I_r[/MATH] ... And once again, [MATH]SAT[/MATH] requires the bottom rows to be null matrices...
\(\displaystyle A\) has rank [MATH] r(A) = r[/MATH].
Prove that if both [MATH]S[/MATH] and [MATH]T[/MATH] are invertible such that [MATH] SAT_{m \times n} =[/MATH]
For starters,
If [MATH]r = m[/MATH], then I don't understand the need for two null matrices in the bottom rows because [MATH]I_{r}[/MATH] occupies all rows. The same goes for [MATH]r = n[/MATH] but for columns...
After this point, I don't really know how to approach this problem and need some guidance.
My first thought was to try and see what happens if [MATH]AT =[/MATH]
