Question with my homework

[bilius2007]

For number 2, instead of ST II UV, shouldn't it be ST II UV? Thanks.

 

[Steven G]

Your proof looks good to me. Your question makes no sense since replacing ST II UV with ST II UV will not change anything.

Please post back and ask the question that you meant to ask.

 

[bilius2007]

I'm sorry, I meant ST II VU

 

[Steven G]

I'm sorry, I meant ST II VU

UV is a line segment that goes between points U and V. VU is a line segment that goes between points V and U. What do you think the difference between UV and VU is? Please post back.

 

[bilius2007]

There is no difference, I just thought that you were supposed to write it with the same notation

 

[bilius2007]

Like if you go from s-t, then you need to go from v-u

 

[Steven G]

There is no difference, I just thought that you were supposed to write it with the same notation

Same notation as ....?

 

[Steven G]

Like if you go from s-t, then you need to go from v-u

So there is a law where if you go from s to t you MUST go from v to u? Why is that? What is the punishment for going from s to t without going from v to u?

 

[Otis]

Like if you go from s-t, then you need to go from v-u

Hi bilius. We're not "going" from point to point, in this exercise. For example, the distance from s to t is simply a length measurement. There is no direction involved.

Later, if you study a different kind of measurement known as 'vector', you will learn about directed distances. Vectors are numbers (measurements) that point in a specific direction, in addition to having a magnitude (length).

For now, UV represents VU (they are interchangeable).

?

 

[bilius2007]

I don't know, but my teacher took points of my test for not doing that, so thats why I thought that.

 

[bilius2007]

Anyway, thanks.

 

[Otis]

… teacher took points [off] my test for [writing UV instead of VU, for example]…

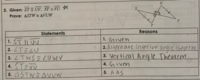
Can you upload an image of what the teacher wrote on your exam? Perhaps, we could see something that might explain.

?

 

[bilius2007]

 

[bilius2007]

Here you go!

 

[Dr.Peterson]

For number 2, instead of ST II UV, shouldn't it be ST II UV? Thanks.

I'm sorry, I meant ST II VU

Like if you go from s-t, then you need to go from v-u

Here is the problem:


Even if direction mattered, ST and UV go in the same direction, so \(ST || UV\) would be appropriate.

I suspect you are confusing parallelism with congruence. At step 4 they say \(ST \cong VU\), which is correct, because in the triangles S corresponds with V and T with U. There that it would be technically a little wrong to write \(ST \cong UV\), not in itself but in preparation for the next step.

In the example you just gave, it is not a segment, but a triangle that is marked wrong -- because there it really makes a difference. Corresponding parts must be correct when you state a congruence of triangles.