logistic_guy
Senior Member
- Joined
- Apr 17, 2024
- Messages
- 2,214
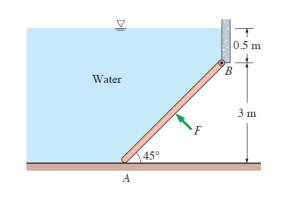
The \(\displaystyle 280\)-\(\displaystyle \text{kg}\), \(\displaystyle 6\)-\(\displaystyle \text{m}\)-wide rectangular gate shown in the figure is hinged at \(\displaystyle B\) and leans against the floor at \(\displaystyle A\) making an angle \(\displaystyle 45^{\circ}\) with the horizontal. The gate is to be opened from its lower edge by applying a normal force at its center. Determine the minimum force \(\displaystyle F\) required to open the water gate.