Scalene Triangle Without Sin or Cos Rules?

[TreasureDragon]

Hello everyone,

I've found this forum to be strict yet helpful group and I am glad to come back! This time, I have two questions regarding Scalene Triangles and Circles.

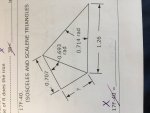
The first question asks for the length of one of the sides when an isosceles and scalene triangles are put together with a few angles and sides given. I assumed this to be a question asking to use Sin or Cos rules but I cannot apply either as they do not meet the requirements to use them. Maybe it was Heron's formula, but to no avail, it was not.


The second question involves an inscribed circle within a scalene triangle. I have never in my life been able to solve a problem like this before. My only problem here is what the relation between the radius of the circle has with the angles/sides of the triangle.


Thank you for the help! PS Please disregard the attached file. Here's the link with both questions as I'm having issues uploading them directly here.

< links to objectionable pages removed >

 

[ksdhart2]

For the second problem, with the circle and the scalene triangle, it appears the circle is supposed to be the incircle of the triangle. That is to say, the largest possible circle that fits fully inside the triangle. If you need a refresher on how to find the radius of a triangle's incircle, try this page from MathOpenRef.

However, the first problem has me a bit stumped at the moment. I sort of feel like I'm missing something obvious, but I'm not sure how to proceed either. About the only thing I can think of is that, since the title is "isoceles and scalene triangles," you're meant to infer that one of the triangles is isoceles and thus one of the non-labeled lengths is either 0.707 (a decimal approximation of sqrt(1/2) perhaps?) or 1.26. If you know what the answer is, maybe you can work your way backwards to the logic... perhaps start by assuming that the 1.26 triangle is the isoceles one. What happens if the shared side's length is 1.26? What happens if the non-shared side length is 1.26? Or, assume that the 0.707 triangle is the isoceles one. What happens if the shared side is 0.707?

 

[TreasureDragon]

Thank you so much for the page!! I didn't have any clue how the circle could have related to the triangle in any way... Also, would it help if the answer was provided? It says the answer should be 0.563 ish. I can't quite puzzle my way out through this...

 

[ksdhart2]

Based on the answer given, I conclude that the bigger triangle is supposed to be the isoceles one, and the non-labeled side is also 1.26. Using the Law of Cosines, we can find that the shared side is 0.881. Using the Law of Cosines again, the side we're asked to solve for is 0.564. That's close enough to the given answer to account for rounding errors. Perhaps ask your instructor to be sure we're doing it correctly. I think this is a poorly constructed problem, as diagrams typically indicate side lengths that are meant to be the same length with hash marks.

 

[TreasureDragon]

Yes, the test creator is infamously known for bad wordings and poorly drawn geometry questions... But I appreciate your help! That circle inside triangle is a real life-saver!!