I have to use the shell method to find the volume between y=-x+9 and y=2x-3 but only the region in the first quadrant.
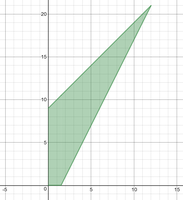
So the graph would look like this:

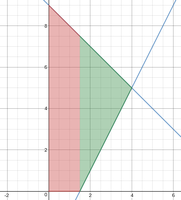
I set up the integral as 2π∫[x((-x+9)-(2x-3))]dx from [0, 4] but I think that would also include that triangle region that's not in the first quadrant?
How would you write the integral so that it doesn't?
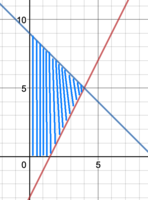
So the graph would look like this:

I set up the integral as 2π∫[x((-x+9)-(2x-3))]dx from [0, 4] but I think that would also include that triangle region that's not in the first quadrant?
How would you write the integral so that it doesn't?