You are using an out of date browser. It may not display this or other websites correctly.
You should upgrade or use an alternative browser.
You should upgrade or use an alternative browser.
Show that tangent function is tangent to unit circle
- Thread starter Mondo
- Start date
BigBeachBanana
Senior Member
- Joined
- Nov 19, 2021
- Messages
- 2,277
[imath]\tan(\theta)[/imath] is not the hypotenuse, but the opposite side of the triangle OAE.Hello,
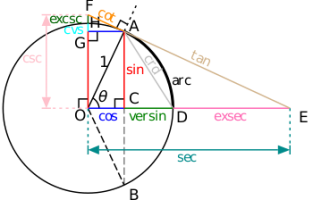
I stumbled upon this graphics which shows various trigonometric functions on a unit circle.
View attachment 33305
I wonder how could we show that tangent function [imath]tan = \frac{sin(\theta)}{cos(\theta)}[/imath] is really the hypotenuse of the big triangle OAE?
Thanks
[math]\cos(\theta)=\frac{adj}{hyp}=\frac{OA}{OE}=\frac{1}{OE} \implies OE=\frac{1}{\cos(\theta)}=\sec(\theta)\\ \sin(\theta)=\frac{opp}{hyp}=\frac{AE}{OE}=\frac{AE}{\sec(\theta)}\implies AE = \sin(\theta)\sec(\theta)=\frac{\sin(\theta)}{\cos(\theta)}=\tan(\theta)[/math]
pka
Elite Member
- Joined
- Jan 29, 2005
- Messages
- 11,990
Look at this plot.Hello,
I stumbled upon this graphics which shows various trigonometric functions on a unit circle.
View attachment 33305
I wonder how could we show that tangent function [imath]tan = \frac{sin(\theta)}{cos(\theta)}[/imath] is really the hypotenuse of the big triangle OAE?
Do you still say that the tangent function is tangent to to the unit circle?
Thank you @BigBeachBanana that's it.
Anyway, thank you for showing an alternative view on the question
Right my mistake.tan(θ) is not the hypotenuse, but the opposite side of the triangle OAE.
@pka heh you show a graph of tangent function with some ellipse fit into it. This is not what I meant. My question was about a unit circle with cos and sin functions well defined and now prove is needed that tangent function is really the segment shown on the graph from first post.Look at this plot.
Do you still say that the tangent function is tangent to to the unit circle?
Anyway, thank you for showing an alternative view on the question
BigBeachBanana
Senior Member
- Joined
- Nov 19, 2021
- Messages
- 2,277
FYI: If you want to partially quote a post, highlight the part you want to quote with your mouse. A small "reply" icon will pop up.Thank you @BigBeachBanana that's it.