similar triangle: parabola w/ focus F, tangents at A, B meet at S

[shahar]

two tangent line of parabola with the focus F, tangent in points A & B and meet s point S, create similar triangle.

How can I prove it?

 

[shahar]

picture

The picture

 

[Dr.Peterson]

Two tangent lines of parabola with the focus F, tangent in points A & B and meet at point S, create similar triangle.

How can I prove it?

Which triangles are you saying are similar?

And what have you tried?

 

[shahar]

my solution

It's from an article.
The similar triangles FSB ~ FSA.
I only the picture and not the article.

If I remember correctly, I need to build 2 right angles. (the sign _|_ is perpendicular)
AH _|_ l (AH perpendicular to l)
BH _l_ l (BH perpendicular to l)
(Question: why it allow?)

So what I need to use, to solve the problem?!

 

[Dr.Peterson]

It's from an article.
The similar triangles FSB ~ FSA.
I only the picture and not the article.

If I remember correctly, I need to build 2 right angles. (the sign _|_ is perpendicular)
AH _|_ l (AH perpendicular to l)
BH _l_ l (BH perpendicular to l)
(Question: why it allow?)

So what I need to use, to solve the problem?!

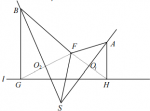
I drew the figure, and confirmed my expectation that in fact FSB ~ FAS, not FSA. The order is important!

When you say "If I remember correctly", are you saying the article gave a proof, or are you just remembering general techniques that might apply here? Presumably you meant to say (as the drawing shows) that AH and BG are perpendicular to the horizontal axis.

But the important thing for me is that you are clearly thinking in terms of synthetic geometry (proving from theorems) rather than analytic geometry and calculus. That tells me what to suggest. But to do this, you have to start with a definition of what it means to be a parabola. You haven't drawn the directrix, which is essential to the focus-directrix definition. In the following figure, I have included the directrix and perpendiculars to the tangents, which suggest some very important relationships based on the definition.



I have not completed a proof yet, but I am familiar with related proofs, and think this will be a good start. See what you can do with it.

 

[yma16]

To start, try to use reflection property to show AQ1 _|_FH

The picture

https://www.youtube.com/watch?v=1befoZdpVMk

In your picture, you need to know that I is the directrix so that you can use the definition of parabola to get mFA=mAH.

The same is true for BQ2.

Thus, in triangle GFH, AQ1 and BQ2 are two perpendicular bisectors. Therefore S is the circumcenter of triangle GFH.

Let the intersection of BS and GH be C. Then each triangle BGQ2 and GQ2C is similar to triangle BGC because they have a common angle and a right angle. Therefore triangles BGQ2 and GQ2C are similar. This gives <GBQ2=<Q2GC.

Now, think about a circle formed by joining G,F,H with center S. Then, <Q2GC=<FGH=1/2<FSH, since <FGH and <FSH face the same arc of the circle.

Triangle AFH is isolelace and AQ1 is a perpendicular bisectors, thus triangle FSQ1 is congruent to triangle SHQ1 (SAS). So we get <FSQ1=1/2FSH.

So, we get <FBQ2=<GBQ2=<Q2GC<FGH=1/2<FSH=<FSQ1.

Similarly, we can show the same for an other angle.