simple electric circuit

[logistic_guy]

Given the electric network shown in the Figure.



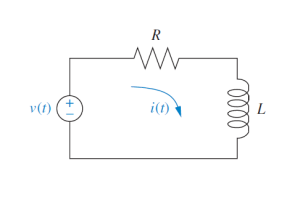
\(\displaystyle {\bold{a.}}\) Write the differential equation for the network if \(\displaystyle v(t) = u(t)\), a unit step.
\(\displaystyle {\bold{b.}}\) Solve the differential equation for the current, \(\displaystyle i(t)\), if there is no initial energy in the network.
\(\displaystyle {\bold{c.}}\) Make a plot of your solution if \(\displaystyle R/L = 1\).

 

[logistic_guy]

\(\displaystyle {\bold{a.}}\) Write the differential equation for the network if \(\displaystyle v(t) = u(t)\), a unit step.

\(\displaystyle v(t) - i(t)R - L\frac{di(t)}{dt} = 0\)

\(\displaystyle u(t) - i(t)R - L\frac{di(t)}{dt} = 0\)

Or

\(\displaystyle \textcolor{blue}{L\frac{di(t)}{dt} + i(t)R = u(t)}\)

 

[logistic_guy]

\(\displaystyle {\bold{b.}}\) Solve the differential equation for the current, \(\displaystyle i(t)\), if there is no initial energy in the network.

If there is no initial energy, then \(\displaystyle i(0) = 0\).

\(\displaystyle L\frac{di(t)}{dt} + i(t)R = u(t)\)

\(\displaystyle u(t) = 1\) for \(\displaystyle t \geq 0\), then

\(\displaystyle L\frac{di(t)}{dt} + i(t)R = 1\)

We will solve this differential equations in two ways. The \(\displaystyle \textcolor{blue}{\text{easy way}}\) and the the \(\displaystyle \textcolor{red}{\text{hard way}}\).

We start with the \(\displaystyle \textcolor{blue}{\bold{easy \ way}}\).

I will use \(\displaystyle i\) instead of \(\displaystyle i(t)\) to save some ink.

\(\displaystyle L\frac{di}{dt} + iR = 1\)


\(\displaystyle L\frac{di}{dt} = 1 - iR\)


\(\displaystyle \frac{di}{dt} = \frac{1 - iR}{L} = \frac{1}{L}(1 - iR)\)


\(\displaystyle \frac{1}{(1 - iR)} \ di = \frac{1}{L} \ dt\)


\(\displaystyle \int_{0}^{i} \frac{1}{(1 - iR)} \ di = \int_{0}^{t} \frac{1}{L} \ dt\)


\(\displaystyle \frac{1}{-R}\ln(1 - iR) = \frac{1}{L}t\)


\(\displaystyle \ln(1 - iR) = -\frac{R}{L}t\)


\(\displaystyle 1 - iR = e^{-\frac{R}{L}t}\)


\(\displaystyle iR - 1 = -e^{-\frac{R}{L}t}\)


\(\displaystyle iR = 1 - e^{-\frac{R}{L}t}\)


\(\displaystyle i(t) = \frac{1 - e^{-\frac{R}{L}t}}{R} = \textcolor{blue}{\frac{1}{R}\left(1 - e^{-\frac{R}{L}t}\right)}\)

 

[logistic_guy]

\(\displaystyle {\bold{b.}}\) Solve the differential equation for the current, \(\displaystyle i(t)\), if there is no initial energy in the network.

Now we solve it by the \(\displaystyle \textcolor{red}{\bold{hard \ way}}\).

\(\displaystyle L\frac{di(t)}{dt} + i(t)R = 1\)


\(\displaystyle \frac{di}{dt} + \frac{R}{L}i = \frac{1}{L}\)


\(\displaystyle e^{\int \frac{R}{L} dt}\frac{di}{dt} + e^{\int \frac{R}{L} dt}\frac{R}{L}i = e^{\int \frac{R}{L} dt}\frac{1}{L}\)


\(\displaystyle \frac{d}{dt}\left(e^{\int \frac{R}{L} dt}i\right) = e^{\int \frac{R}{L} dt}\frac{1}{L}\)


\(\displaystyle d\left(e^{\int \frac{R}{L} dt}i\right) = e^{\int \frac{R}{L} dt}\frac{1}{L} \ dt\)


\(\displaystyle \int d\left(e^{\int \frac{R}{L} dt}i\right) = \int e^{\int \frac{R}{L} dt}\frac{1}{L} \ dt\)


\(\displaystyle e^{\int \frac{R}{L} dt}i = \frac{L}{R} e^{\int \frac{R}{L} dt}\frac{1}{L} + c_1\)


\(\displaystyle i = \frac{1}{R} + c_1e^{-\int \frac{R}{L} dt}\)


\(\displaystyle i = \frac{1}{R} + c_1e^{-\frac{R}{L}t + c_2}\)


\(\displaystyle i = \frac{1}{R} + c_3e^{-\frac{R}{L}t}\)


Apply \(\displaystyle i(0) = 0\).


\(\displaystyle 0 = \frac{1}{R} + c_3\)


\(\displaystyle c_3 = -\frac{1}{R}\), then


\(\displaystyle i(t) = \frac{1}{R} - \frac{1}{R}e^{-\frac{R}{L}t} =\textcolor{red}{\frac{1}{R}\left(1 - e^{-\frac{R}{L}t}\right)}\)

 

[logistic_guy]

\(\displaystyle {\bold{c.}}\) Make a plot of your solution if \(\displaystyle R/L = 1\).

I will choose \(\displaystyle R = L = 1\).

\(\displaystyle i(t) = 1 - e^{-t}\)