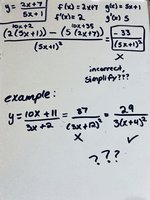I was give the problem (2x+7)/(5x+1) and used the quotient rule and got got -33/(5x+1)^2. However it was marked incorrect. I remember we were supposed to take something out of the answer (denominator) to further simplify it but I’m not sure what goes into -33, certainly not a 5 so I’m lost.
You are using an out of date browser. It may not display this or other websites correctly.
You should upgrade or use an alternative browser.
You should upgrade or use an alternative browser.
Simplifying Quotient Derivatives help
- Thread starter KG17
- Start date
Dr.Peterson
Elite Member
- Joined
- Nov 12, 2017
- Messages
- 16,855
Note how I've added words to your statement of the problem. A function is not a problem; and differentiation is not a trivial thing to be left unsaid.I was give the problem to differentiate the function (2x+7)/(5x+1) and used the quotient rule and got got -33/(5x+1)^2. However it was marked incorrect. I remember we were supposed to take something out of the answer (denominator) to further simplify it but I’m not sure what goes into -33, certainly not a 5 so I’m lost.
You similarly omitted information from the example you gave. Don't use "=" between things that are not equal.
Here is what it should say, with a step or two inserted for clarity and a number corrected:
[MATH]y = \frac{10x+11}{3x+12}[/MATH]; [MATH]y' = \frac{87}{(3x+12)^2} = \frac{87}{(3(x+4))^2} = \frac{3(29)}{9(x+4)^2} = \frac{29}{3(x+4)^2}[/MATH]
This shows how to deal with a common factor in the denominator. But your problem at the top has no such common factor, either within the denominator, or between numerator and denominator (33 = 3*11), so I would leave it exactly as you did. See here. Are you sure you copied the problem correctly, and there were no additional instructions as to what form was required?
Steven G
Elite Member
- Joined
- Dec 30, 2014
- Messages
- 14,596
Oops, the 9 should not be part of the square. I meant to write 87/[9(x+4)2]The top derivative is correct.
I am completely confused why you think (10x+11)/(3x+2) should equal 87/(3x+12)2
Now 87/(3x+12)2 = 87/[3(x+4)]2 = 87/[9(x+4)]2
You need to square the 3!!
Sorry my set up was sloppy but this was the original question (has yet to be solved)Note how I've added words to your statement of the problem. A function is not a problem; and differentiation is not a trivial thing to be left unsaid.
You similarly omitted information from the example you gave. Don't use "=" between things that are not equal.
Here is what it should say, with a step or two inserted for clarity and a number corrected:
[MATH]y = \frac{10x+11}{3x+12}[/MATH]; [MATH]y' = \frac{87}{(3x+12)^2} = \frac{87}{(3(x+4))^2} = \frac{3(29)}{9(x+4)^2} = \frac{29}{3(x+4)^2}[/MATH]
This shows how to deal with a common factor in the denominator. But your problem at the top has no such common factor, either within the denominator, or between numerator and denominator (33 = 3*11), so I would leave it exactly as you did. See here. Are you sure you copied the problem correctly, and there were no additional instructions as to what form was required?

Dr.Peterson
Elite Member
- Joined
- Nov 12, 2017
- Messages
- 16,855
Ah! So you got a sign wrong. It isn't (2x+7)/(5x+1), but (2x+7)/(5x-1).
Have you redone your work for the correct problem?
Have you redone your work for the correct problem?
Oh okay so....[MATH]y=\frac{2x+7}{5x-1} [/MATH] So basically In your answer the bottom part is almost correct[MATH](5x-1)^2[/MATH] (I changed the + sign to a -)it's mainly the top of part which is wrong (33) [MATH]y′=\frac{work this out} {(5x-1)^2}[/MATH] if you simplify this you should get your answer....[MATH]y′=\frac{2(5x-1)-(2x+7)\times5}{(5x-1)^2}[/MATH]