logistic_guy
Senior Member
- Joined
- Apr 17, 2024
- Messages
- 2,214
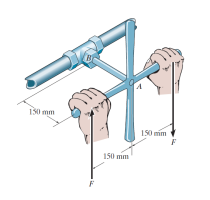
If the solid shaft \(\displaystyle AB\) to which the valve handle is attached is made of \(\displaystyle \text{C83400}\) red brass and has a diameter of \(\displaystyle 10 \ \text{mm}\), determine the maximum couple forces \(\displaystyle F\) that can be applied to the handle just before the material starts to fail. Take \(\displaystyle \tau_{\text{allow}} = 40 \ \text{MPa}\). What is the angle of twist of the handle? The shaft is fixed at \(\displaystyle A\).