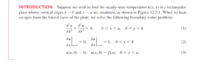Solution of Laplace Eq.

[shreddinglicks]

I am studying an example problem in my textbook that determines a solution of Laplaces equation applied to a flat plate. I have attached the final solution. I have no issue obtaining the summation term. I don't understand how the first term comes about. If I take n = o, I get sinh(0) = 0.
How does the book have the term written as Asub0 * y ? Is there a trick applied to the summation term?

 

[Romsek]

going to have to see the entire problem

 

[shreddinglicks]

Here is the example up to the point in question.

 

[Romsek]

Ok. It looks like the \(\displaystyle A_0y\) term comes from the solution to the \(\displaystyle \lambda=0\) case that they have added via superposition to the solution for the \(\displaystyle \lambda \neq 0\) case.

The sums run from \(\displaystyle n=1\to \infty\) so the hyperbolic sine is never evaluated at 0.

 

[shreddinglicks]

I see what you mean. I find it confusing that near the end it is written Asub0*y, n = 0. That makes me take the summation term and plug in n = 0 which gives 0.