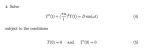Looks straightforward to me. Are you learning anything from the responses to your posts?
The differential equation is \(\displaystyle T''(t)+ \left(\frac{\pi a}{l}\right)^2T(t)= D sin(\omega t)\). The associated homogeneous differential equation is \(\displaystyle T''(t)+ \left(\frac{\pi a}{l}\right)^2T(t)= 0\). It's characteristic equation is \(\displaystyle \lambda^2+ \left(\frac{\pi a}{l}\right)^2= 0\) which has roots \(\displaystyle \lambda= \frac{\pi a}{l} i\). So the general solution to the associated homogeneous differential equation is \(\displaystyle C_1 cos\left(\frac{\pi a}{l}t\right)+ C_2 sin(\left(\frac{\pi a}{l}t\right)\).
Now the right hand side of the original non-homogeneous equation is \(\displaystyle D sin(\omega t)\). What we do now depends upon what \(\displaystyle \omega t\) is! If \(\displaystyle \omega\ne \frac{\pi a}{l}\) then we look for a particular solution of the form \(\displaystyle T(t)= A cos(\omega t)+ B sin(\omega t)\). Then \(\displaystyle T'= -A\omega sin(\omega t)+ B\omega cos(\omega t)\) and then \(\displaystyle T''= -A\omega^2 cos(\omega t)- B\omega^2 sin(\omega t)\) and the equation becomes \(\displaystyle T''= -A\omega^2 cos(\omega t)- B\omega^2 sin(\omega t)+ \left(\frac{\pi a}{l}\right)^2(A cos(\omega t)+ B sin(\omega t))= \left(-A\omega^2+ \left(\frac{\pi a}{l}\right)^2\right) cos(\omega t)+ \left(B\omega^2+ \left(\frac{\pi a}{l}\right)^2\right) sin(\omega t)= D sin(\omega t)\).
So we must have \(\displaystyle \left(-\omega^2+ \left(\frac{\pi a}{l}\right)^2\right)A= 0\) and \(\displaystyle \left(\omega^2+ \left(\frac{\pi a}{l}\right)^2\right)B= D\). Solve those two equations for A and B (in terms of D).
However, if \(\displaystyle \omega= \frac{\pi a}{l}\) those "collapse". Instead, we need to take, as our particular solution \(\displaystyle T(t)= A tcos(\omega t)+ B tsin(\omega t)\). Calculate T'' for that and put it into the equation.