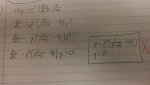Reinofratch
New member
- Joined
- Feb 1, 2016
- Messages
- 1
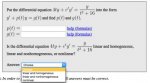
a. Put the differential equation \(\displaystyle \, 4ty\, +\, e^t\, y'\, =\, \dfrac{y}{t^2\, +\, 16}\,\) into the form \(\displaystyle \, y'\, +\, p(t)\, y\, =\, g(t),\,\) and find \(\displaystyle \, p(t)\,\) and \(\displaystyle g(t).\)
b. Is the differential equation \(\displaystyle \, 4ty\, +\, e^t\, y'\, =\, \dfrac{y}{t^2\, +\, 16}\,\) linear and homogeneous, linear and nonhomogeneous, or nonlinear?
I have been trying to solve this question for a week but I can not figure out where I am going wrong:
\(\displaystyle 4ty\, +\, e^t\, \left(\dfrac{dy}{dx}\right)\, =\, \dfrac{y}{t^2\, +\, 16}\)
\(\displaystyle \dfrac{dy}{dx}\, =\, \dfrac{1}{e^t}\, \left(\dfrac{y}{t^2\, +\, 16}\, -\, 4ty\right)\)
\(\displaystyle \dfrac{dy}{dx}\, =\, y\, \left(\dfrac{1}{t^2\, +\, 16}\, -\, 4t\right)\, e^t\)
\(\displaystyle \dfrac{dy}{dx}\, -\, e^t\, \left(\dfrac{1}{t^2\, +\, 16}\, -\, 4t\right)\, y\, =\, 0\)
\(\displaystyle p\, =\, e^t\, \left(\dfrac{1}{t^2\, +\, 16}\, -\, 4t\right)\, \mbox{ and }\, g\, =\, 0\). .<== these were marked wrong
b. Is the differential equation \(\displaystyle \, 4ty\, +\, e^t\, y'\, =\, \dfrac{y}{t^2\, +\, 16}\,\) linear and homogeneous, linear and nonhomogeneous, or nonlinear?
I have been trying to solve this question for a week but I can not figure out where I am going wrong:
\(\displaystyle 4ty\, +\, e^t\, \left(\dfrac{dy}{dx}\right)\, =\, \dfrac{y}{t^2\, +\, 16}\)
\(\displaystyle \dfrac{dy}{dx}\, =\, \dfrac{1}{e^t}\, \left(\dfrac{y}{t^2\, +\, 16}\, -\, 4ty\right)\)
\(\displaystyle \dfrac{dy}{dx}\, =\, y\, \left(\dfrac{1}{t^2\, +\, 16}\, -\, 4t\right)\, e^t\)
\(\displaystyle \dfrac{dy}{dx}\, -\, e^t\, \left(\dfrac{1}{t^2\, +\, 16}\, -\, 4t\right)\, y\, =\, 0\)
\(\displaystyle p\, =\, e^t\, \left(\dfrac{1}{t^2\, +\, 16}\, -\, 4t\right)\, \mbox{ and }\, g\, =\, 0\). .<== these were marked wrong
Attachments
Last edited by a moderator: