Calculator
New member
- Joined
- Apr 27, 2014
- Messages
- 12
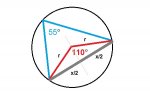
If the radius of the circle is 10 cm, and the inscribed angle is 55 degrees, find the length of the subtended chord.
This is what I did:
tan(55) = h/5
h = 7, 14 cm
and now using the Pythagorean theorem: x^2 =h^2+5^2
x =8, 7 cm
where h is the height of the triangle,
and x is the chord(i.e. one side of the triangle?)
Is this correct?
This is what I did:
tan(55) = h/5
h = 7, 14 cm
and now using the Pythagorean theorem: x^2 =h^2+5^2
x =8, 7 cm
where h is the height of the triangle,
and x is the chord(i.e. one side of the triangle?)
Is this correct?
Last edited: