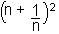OK, these are the ones that I'm having trouble with...which is all of them. :roll: I tried searching for these questions already on this forum, and something came up on Google, but the post didn't exist when I clicked on the result. 
1) Mathman goes to Math R Us to buy a textbook and a graphing calculator. He notices that the sum of the list prices of the two items is $132.50. The store manager, Ray D. Cal, will give a 25% discount on the textbook, but no discount on the calculator. After the discount is figured and 7% sales tax is added to the purchases, to Mathman's amazement, the bill comes to exactly the same value as the original sum of the list prices ($132.50). What is the list price of the calculator? Give your answer to the nearest cent.
2) A complex number has the form a + bi. If this complex number is multiplied but its conjugate the result is 221. If the original complex number a + bi is squared, the result is 171 - 140i. What is the value of |a| + |b| ? (I should be able to figure this one out considering that we're on imaginary numbers in Pre-Calculus right now, but I can't. )
)
3) The cost of a gallon of gasoline is due three things (contrary to popular belief, gas prices are not random [yes, this was actually in the question]):
4) If ( n + [1/n] )^2 = 5 , then find n^3 + 1/(n^3) .
I would graciously any and all help that could be provided, so help me, please!
1) Mathman goes to Math R Us to buy a textbook and a graphing calculator. He notices that the sum of the list prices of the two items is $132.50. The store manager, Ray D. Cal, will give a 25% discount on the textbook, but no discount on the calculator. After the discount is figured and 7% sales tax is added to the purchases, to Mathman's amazement, the bill comes to exactly the same value as the original sum of the list prices ($132.50). What is the list price of the calculator? Give your answer to the nearest cent.
2) A complex number has the form a + bi. If this complex number is multiplied but its conjugate the result is 221. If the original complex number a + bi is squared, the result is 171 - 140i. What is the value of |a| + |b| ? (I should be able to figure this one out considering that we're on imaginary numbers in Pre-Calculus right now, but I can't.
3) The cost of a gallon of gasoline is due three things (contrary to popular belief, gas prices are not random [yes, this was actually in the question]):
- The cost to manufacture (drilling, transporting, refining).[/*:m:2kxkjts9]
- State and local taxes.[/*:m:2kxkjts9]
- Profits (manufacturers and retailers).[/*:m:2kxkjts9]
4) If ( n + [1/n] )^2 = 5 , then find n^3 + 1/(n^3) .
I would graciously any and all help that could be provided, so help me, please!