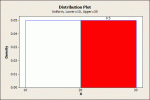
The uniform distribution is a rectangle. That is what makes it easy to deal with. The probability is uniform across the distribution.
Take P(20<x<30). The entire rectangle ranges from 10 to 30. The area of the whole rectangle is 1, as it should be.
20 to 30 is half of the rectangle, so P(20<x<30)=.50
How about \(\displaystyle P(10\leq x\leq 25)\)?. How much area is this. (25-10)=15, 30-10=20
15/20=.75
Or think of it as the rectangle having a height of .05 and the length of what is given. \(\displaystyle \underbrace{.05}_{\text{f(x)}}(25-10)=.75\)
Now, see what to do?. Do the others.
The mean of a uniform distribution is \(\displaystyle \mu=\frac{c+d}{2}=\frac{30+10}{2}=20\). Just as they gave.
The standard deviation is \(\displaystyle \sigma=\sqrt{\frac{1}{12}(d-c)^{2}}=\sqrt{\frac{1}{12}(30-10)^{2}}=5.77\). Just as they gave.
Here is a Minitab graph of P(20<x<30):