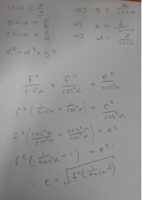Rob Edwards
New member
- Joined
- Aug 22, 2020
- Messages
- 12
Hello again Math Wizards.
For context this is a subsequent problem I am facing after the first problem was solved here
I am attempting to work out how many diamonds I need of a given proportion of no greater than a maximum width to fill a designated total width.
The diamonds have a border of known size.
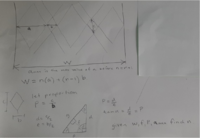
Here's an image that hopefully paints a clearer picture n is the number of panels of width a
So far I have reduced the problem to

From here
I know that the proportion is equal to the tangent and I know f (it is half the border width) so if I can solve this I think I can manage the rest.
With the following as a starting point I've tried all the obvious things in my limited repertoire.
p = d / e = tan(a)
g^2 = e^2 + d^2
d = f / cos(a)
e = f / sin(a)
sin(a) = d / g
cos(a) = e / g
It's way above my pay grade.. Any help would be greatly appreciated
For context this is a subsequent problem I am facing after the first problem was solved here
Stuck designing a diamond pattern leaded window.
Hello everyone. This is my first post - apologies if I don't follow correct forum etiquette. I am a traditional woodworker designing a window in CAD. My maths is very rusty (30 years since I did A-Levels in the UK) I attach a picture of the problem I'm trying to solve and repeat the...
www.freemathhelp.com
I am attempting to work out how many diamonds I need of a given proportion of no greater than a maximum width to fill a designated total width.
The diamonds have a border of known size.
Here's an image that hopefully paints a clearer picture n is the number of panels of width a

So far I have reduced the problem to

From here
I know that the proportion is equal to the tangent and I know f (it is half the border width) so if I can solve this I think I can manage the rest.
With the following as a starting point I've tried all the obvious things in my limited repertoire.
p = d / e = tan(a)
g^2 = e^2 + d^2
d = f / cos(a)
e = f / sin(a)
sin(a) = d / g
cos(a) = e / g
It's way above my pay grade.. Any help would be greatly appreciated