Just to make sure we aren't adding confusion:
The original question was,
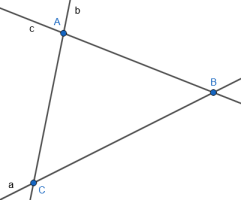
Given:
Line a intersects line b.
Line b intersects line c.
Conclusion:
Line c intersects line a.
The AI give me that isn't true, but I don't understand the explaining, so I publish it to get a human eye.
How can I prove the conclusion is false?
The AI is correct in saying the conclusion does not follow from the givens, whether the context is planar or not. Presumably that is the expected answer.
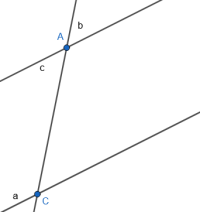
The easiest proof of that is a counterexample where a and c are parallel (everything in one plane), and that is sufficient. More generally, a and c could be skew lines that both intersect b, though it isn't necessary to think in that direction, and that would not be appropriate if the problem were explicitly in plane geometry.
If we were told what explanation the AI gave, there might be more to discuss.
This is one problem with AI - you must define the problem exactly. You must include - " No 3-D consideration" to get the answer you are expecting (for this problem).
Of course, this is actually the problem with
any problem! Whether AI is involved or not, an exact statement is needed. And when we are not told the context, we need to ask. If it actually mattered, hopefully we, or the AI, would have asked.
"Thinking about two lines not intersecting should immediately suggest (in fact, imply!) two parallel lines."
You could also think about skew lines if another dimension is allowed.
You're exactly right. Without knowing this, my word "suggest" is appropriate, but "imply" was not. I was assuming the simplest possible context.
Knowing the context would certainly help, though it wouldn't change the answer.