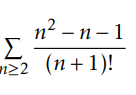You are using an out of date browser. It may not display this or other websites correctly.
You should upgrade or use an alternative browser.
You should upgrade or use an alternative browser.
Sum of a series
- Thread starter Bogdan73
- Start date
pka
Elite Member
- Joined
- Jan 29, 2005
- Messages
- 11,990
Use the ratio test to prove convergence.View attachment 15022 Can someone help me to fin the sum of this series, maybe step by step?
Here is a partial sum \(\displaystyle {S_m} = \sum\limits_{n = 2}^m {\frac{{{n^2} - n - 1}}{{(n + 1)!}}} = \frac{{(m + 2)! - 2{m^2} - 4m}}{{2(m + 2)!}}\)
Using a basic comparison we can see the sequence of partial sums increases and is bounded.
- Joined
- Nov 24, 2012
- Messages
- 3,021
Okay, now that the partial sum has been given to you, let's see how it can be developed. I would write:
[MATH]S_n=\sum_{k=2}^{n}\left(\frac{k^2-k-1}{(k+1)!}\right)[/MATH]
Using the hint I provided in post #2, we may write:
[MATH]S_n=\sum_{k=2}^{n}\left(\frac{k-1}{k!}-\frac{k}{(k+1)!}\right)[/MATH]
And thus:
[MATH]S_n=\sum_{k=2}^{n}\left(\frac{k-1}{k!}\right)-\sum_{k=2}^{n}\left(\frac{k}{(k+1)!}\right)[/MATH]
Let's re-index the first sum on the right:
[MATH]S_n=\sum_{k=1}^{n-1}\left(\frac{k}{(k+1)!}\right)-\sum_{k=2}^{n}\left(\frac{k}{(k+1)!}\right)[/MATH]
Now, let's pull off the first term of the first sum and the last term of the second sum:
[MATH]S_n=\frac{1}{2}+\sum_{k=2}^{n-1}\left(\frac{k}{(k+1)!}\right)-\sum_{k=2}^{n-1}\left(\frac{k}{(k+1)!}\right)-\frac{n}{(n+1)!}[/MATH]
And since the two sums now add to zero, we're left with:
[MATH]S_n=\frac{1}{2}-\frac{n}{(n+1)!}[/MATH]
Now, can you compute:
[MATH]S_{\infty}=\lim_{n\to\infty}\left(S_n\right)=?[/MATH]
[MATH]S_n=\sum_{k=2}^{n}\left(\frac{k^2-k-1}{(k+1)!}\right)[/MATH]
Using the hint I provided in post #2, we may write:
[MATH]S_n=\sum_{k=2}^{n}\left(\frac{k-1}{k!}-\frac{k}{(k+1)!}\right)[/MATH]
And thus:
[MATH]S_n=\sum_{k=2}^{n}\left(\frac{k-1}{k!}\right)-\sum_{k=2}^{n}\left(\frac{k}{(k+1)!}\right)[/MATH]
Let's re-index the first sum on the right:
[MATH]S_n=\sum_{k=1}^{n-1}\left(\frac{k}{(k+1)!}\right)-\sum_{k=2}^{n}\left(\frac{k}{(k+1)!}\right)[/MATH]
Now, let's pull off the first term of the first sum and the last term of the second sum:
[MATH]S_n=\frac{1}{2}+\sum_{k=2}^{n-1}\left(\frac{k}{(k+1)!}\right)-\sum_{k=2}^{n-1}\left(\frac{k}{(k+1)!}\right)-\frac{n}{(n+1)!}[/MATH]
And since the two sums now add to zero, we're left with:
[MATH]S_n=\frac{1}{2}-\frac{n}{(n+1)!}[/MATH]
Now, can you compute:
[MATH]S_{\infty}=\lim_{n\to\infty}\left(S_n\right)=?[/MATH]