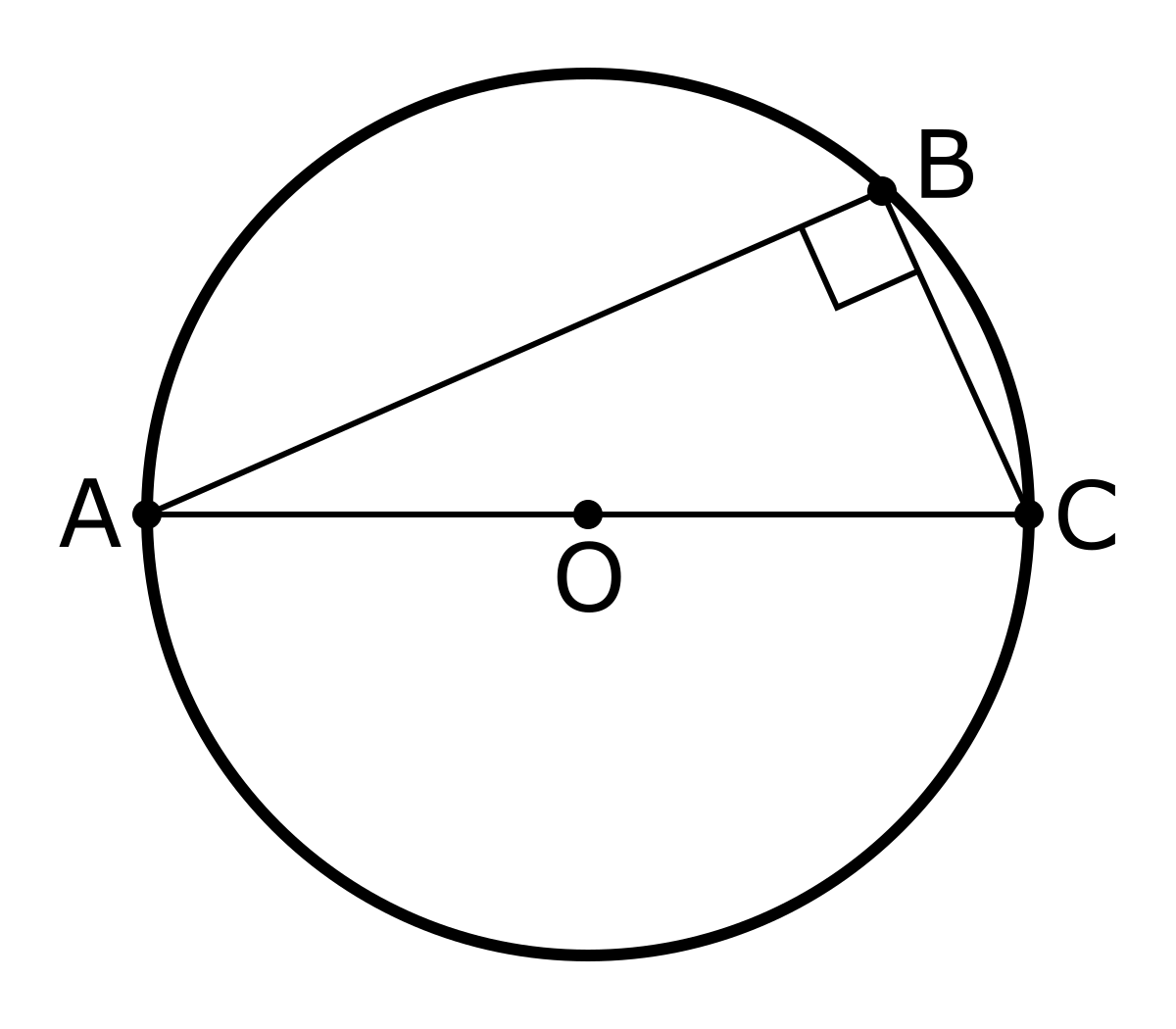
I came across a problem that said a triangle with a right angle is inscribed in the circle. The solution says that because it's a triangle with a right angle in the circle, hypotenuse equals the diameter. Searching about this, since I did not know about it before, I found Thales's theorem which states (according to wiki):
In geometry, Thales' theorem states that if A, B, and C are distinct points on a circle where the line AC is a diameter, the angle ABC is a right angle.
Now this got me confused. According to this because AC is a diameter the angle ABC is a right angle. While my problem states that there is a right angle inscribed in the circle, with no mention of the diameter. The definition suggests that the angle is a right angle if AC is a diameter, but not that necessarily, a right angle has a diameter as hypotenuse. I am confused about this. Did I even find the right theorem? And If I did, what is the proof for it?
In geometry, Thales' theorem states that if A, B, and C are distinct points on a circle where the line AC is a diameter, the angle ABC is a right angle.
Now this got me confused. According to this because AC is a diameter the angle ABC is a right angle. While my problem states that there is a right angle inscribed in the circle, with no mention of the diameter. The definition suggests that the angle is a right angle if AC is a diameter, but not that necessarily, a right angle has a diameter as hypotenuse. I am confused about this. Did I even find the right theorem? And If I did, what is the proof for it?