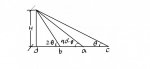
Application of Double Angles (Addition Formulas): The angle of elevation of a wireless telegraph tower is observed from a point on the horizontal plain (plane?) on which it stands. At a point "a" nearer the angle of elevation is the compliment of the former. At a point "b" nearer still, the angle of elevation is double the first. Show that the height of the tower is:
h= [(a+b)^2 - (a/2)^2]^(1/2)
Please!!! Anyone. I need a detailed solution. Thanks
h= [(a+b)^2 - (a/2)^2]^(1/2)
Please!!! Anyone. I need a detailed solution. Thanks
Last edited by a moderator: