I'm finishing that last two chapters of trig on my own over the summer and this one has stumped me for the past few weeks.Find the millionth roots of i and plot your answer.
I know that the resulting graph will be a circle (or technically, a million-sided shape, but close enough). I know I'm supposed to change the algebraic form (i) to the polar form (this is what I'm having trouble with).
I'm supposed to make a graph with a triangle, but the end result I keep getting is 0cos(180)+0isin(180). Obviously, this results in 0.
This is the graph form I'm supposed to be using:
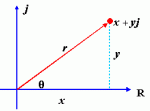
Then I write it in polar form: [FONT=MathJax_Math]x[FONT=MathJax_Main]+[/FONT][FONT=MathJax_Math]y[/FONT][FONT=MathJax_Math]j[/FONT][FONT=MathJax_Main]=[/FONT][FONT=MathJax_Math]r[/FONT][FONT=MathJax_Main]([/FONT][FONT=MathJax_Main]cos[/FONT][FONT=MathJax_Math]θ[/FONT][FONT=MathJax_Main]+[/FONT][FONT=MathJax_Math]j[/FONT][FONT=MathJax_Main]sin[/FONT][FONT=MathJax_Math]θ[/FONT][FONT=MathJax_Main])[/FONT][/FONT]
Then, if I get the polar form, I get to move on to de Moivre's theorem and I can't even understand how that factors in.
Thank you so much if you can help me. I hope I've explained what I have so far well.
Last edited:
