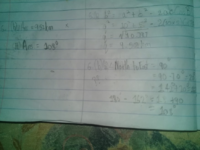This is what I've attempted . In part one, I did the right working and got the wrong answer. ( Obviously it's not the right working then..)So then I tried Cos 20 but can someone help me understand what is Cos 20 and why it works? Is angle P from Q actually 020° ? (i) Ans.= 5.6km
In part 2 I tried ...nonsense. Then I tried 142/2= 71. 90-71 = 19+90= 109 but that was 001 ° off. So.. how? (ii) Ans.= 108°
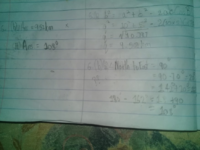
In part 2 I tried ...nonsense. Then I tried 142/2= 71. 90-71 = 19+90= 109 but that was 001 ° off. So.. how? (ii) Ans.= 108°

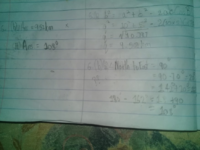
Attachments
Last edited: