logistic_guy
Senior Member
- Joined
- Apr 17, 2024
- Messages
- 2,213
\(\displaystyle \bold{Given}\): \(\displaystyle \Delta \text{ABC is isosceles} \ (\overline{\text{AB}} \ \cong \overline{\text{AC}}). \ Ⓢ \ \text{P and Q}\), \(\displaystyle \overline{\text{BC}} \parallel \overline{\text{PQ}}\).
\(\displaystyle \bold{Prove}\): \(\displaystyle \text{\large$\odot$}\text{P} \ \cong \text{\large$\odot$}\text{Q}\).
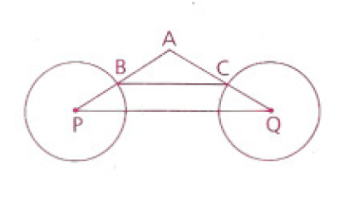
\(\displaystyle \bold{Prove}\): \(\displaystyle \text{\large$\odot$}\text{P} \ \cong \text{\large$\odot$}\text{Q}\).

