logistic_guy
Senior Member
- Joined
- Apr 17, 2024
- Messages
- 2,214
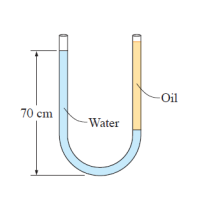
Consider a \(\displaystyle \text{U}\)-tube whose arms are open to the atmosphere. Now water is poured into the \(\displaystyle \text{U}\)-tube from one arm, and light oil \(\displaystyle \left(\rho = 790 \ \text{kg/m}^3\right)\) from the other. One arm contains \(\displaystyle 70\)-\(\displaystyle \text{cm}\)-high water, while the other arm contains both fluids with an oil-to-water height ratio of \(\displaystyle 6\). Determine the height of each fluid in that arm.