logistic_guy
Senior Member
- Joined
- Apr 17, 2024
- Messages
- 2,214
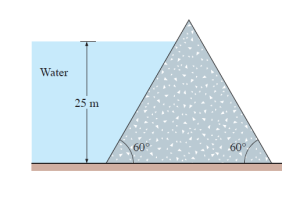
The water in a \(\displaystyle 25\)-\(\displaystyle \text{m}\)-deep reservoir is kept inside by a \(\displaystyle 150\)-\(\displaystyle \text{m}\)-wide wall whose cross section is an equilateral triangle, as shown in the figure. Determine \(\displaystyle \bold{(a)}\) the total force (hydrostatic + atmospheric) acting on the inner surface of the wall and its line of action and \(\displaystyle \bold{(b)}\) the magnitude of the horizontal component of this force. Take \(\displaystyle P_{\text{atm}} = 100 \ \text{kPa}\).