Can someone help me understand the answer to this differential?
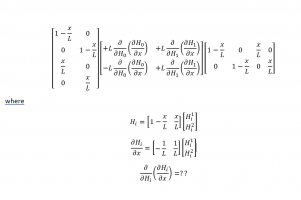
I have the following expression
View attachment 301107where
View attachment 301108
Now what I can understand the differential of
View attachment 301109
what will be the following?
View attachment 301110
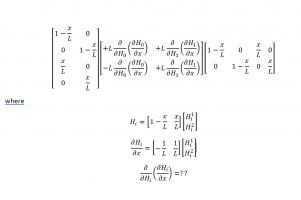
I have the following expression
View attachment 301107where
View attachment 301108
Now what I can understand the differential of
View attachment 301109
what will be the following?
View attachment 301110