Not sure where to post this:
I saw this question in a book:

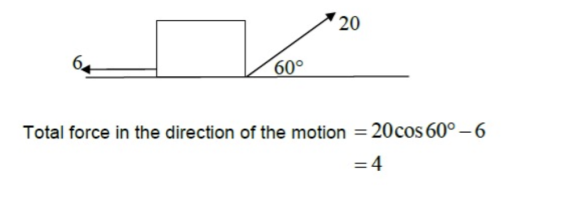
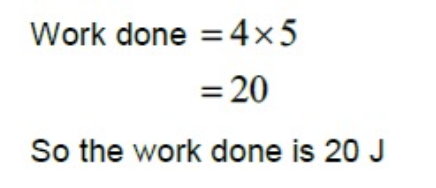
Is this correct? Is it not the case the work done is 50J ( 20cos60 x 5) .some of that of that work (30J) goes towards overcoming friction and some of it (20J) towards increasing KE, but it's all work done. So the answer is 50J.
What does the question mean when it asks 'work done IN...' ?
I saw this question in a book:


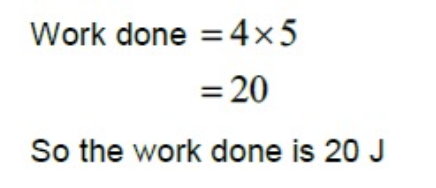
Is this correct? Is it not the case the work done is 50J ( 20cos60 x 5) .some of that of that work (30J) goes towards overcoming friction and some of it (20J) towards increasing KE, but it's all work done. So the answer is 50J.
What does the question mean when it asks 'work done IN...' ?
