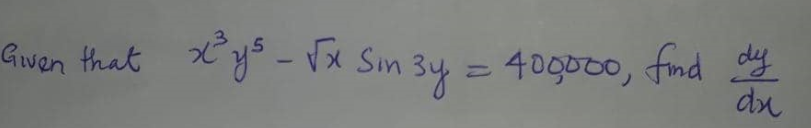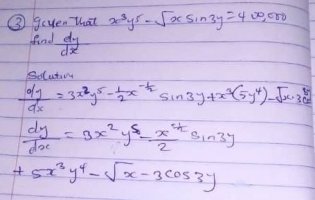You are using an out of date browser. It may not display this or other websites correctly.
You should upgrade or use an alternative browser.
You should upgrade or use an alternative browser.
x^3 y5 - root x sin 3y = 400,000, find dy/dx
- Thread starter ugu
- Start date
Exactly why it is complicated to me too. It seem longer than expectedI have trouble reading your picture. I do not understand your second line. How does that come out of the product rule?
[math]\dfrac{d}{dx}(x^3y^5) = 3x^2y^5 + 5x^3y^4 * \dfrac{dy}{dx}[/math]
What
Well, I cannot explain your work to you. How did yo
WHAT ABOUT THIS?
BigBeachBanana
Senior Member
- Joined
- Nov 19, 2021
- Messages
- 2,277
Is the instruction asking you to find dy/dx using implicit differentiation?
No. When you differentiate a function of y against x, you must use the chain rule. So dy/dx is going to be a factor wherever you differentiate a function of y. Implicit differentiation is a special case of the chain ruleWhat about this?
[math]x^3 * (5y^4) * \dfrac{dy}{dx} + 3x^2y^5 - \dfrac{sin(3y)}{2\sqrt{x}} - 3\sqrt{x} * cos(3y) * \dfrac{dy}{dx} = 0.[/math]
Now solve for dy/dx.
Meaning the second solution is also not correct?No. When you differentiate a function of y against x, you must use the chain rule. So dy/dx is going to be a factor wherever you differentiate a function of y. Implicit differentiation is a special case of the chain rule
[math]x^3 * (5y^4) * \dfrac{dy}{dx} + 3x^2y^5 - \dfrac{sin(3y)}{2\sqrt{x}} - 3\sqrt{x} * cos(3y) * \dfrac{dy}{dx} = 0.[/math]
Now solve for dy/dx.
Not at all
Is the instruction asking you to find dy/dx using implicit differentiations
BigBeachBanana
Senior Member
- Joined
- Nov 19, 2021
- Messages
- 2,277
If the question doesn't ask you to do implicit differentiation, then why are you doing it? Treat y as a constant when differentiating.Not at all
Meaning the second solution is not correct.Meaning the second solution is also not correct?
Why do you say that this is not a problem in implicit differentiation?
What is the name of the topic under which you found this problem?
Implicit and parametric differentiationsMeaning the second solution is not correct.
Why do you say that this is not a problem in implicit differentiation?
What is the name of the topic under which you found this problem?
BigBeachBanana
Senior Member
- Joined
- Nov 19, 2021
- Messages
- 2,277
1) Since it is under the implicit differentiation section, implicit differentiation is implied in the direction.I do not know actually what this course is doing in computer science. I am not assimilating at all. Always lost along the line but I wish to know
2)Calculus is fundamental for all STEM majors
3) Break the problem into smaller pieces

Last edited:
So it is implicit differentiation.Implicit and parametric differentiations
I showed you the first step. Just solve for dy/dx then come back and ask for an explanation of implicit differentiation.
I am sorry to jump in the middle of the discussion, but your response attracted me. Is it really that we can solve this problem without using implicit differentiation? From my knowledge, if we can't solve for \(\displaystyle y\), then we don't have any other option than using implicit differentiation. If you can solve this problem without using implicit differentiation, please enlighten me.If the question doesn't ask you to do implicit differentiation, then why are you doing it? Treat y as a constant when differentiating.
BigBeachBanana
Senior Member
- Joined
- Nov 19, 2021
- Messages
- 2,277
In multivariable calculus, if such a problem were presented, it's a partial derivative. https://www.mathsisfun.com/calculus/derivatives-partial.htmlI am sorry to jump in the middle of the discussion, but your response attracted me. Is it really that we can solve this problem without using implicit differentiation? From my knowledge, if we can't solve for \(\displaystyle y\), then we don't have any other option than using implicit differentiation. If you can solve this problem without using implicit differentiation, please enlighten me.
You mean that the question would be asking forIn multivariable calculus, if such a problem were presented, it's a partial derivative. https://www.mathsisfun.com/calculus/derivatives-partial.html
\(\displaystyle \frac{\partial f}{\partial y}\) or \(\displaystyle \frac{\partial f}{\partial x}\)
If this is the case, the question should be written as
Given that \(\displaystyle f(x,y) = 400000 + \sqrt{x} \sin 3y - x^3 y^5\), find \(\displaystyle \frac{\partial f}{\partial x}\) or even \(\displaystyle \frac{df}{dx}\).
But it was not. It is so clear that it is an implicit differentiation question.
Even if we assume that it is not an implicit differentiation question, \(\displaystyle \frac{dy}{dx}\), doesn't imply to treat \(\displaystyle y\) as a constant.