I am struggling with this Trig problem:
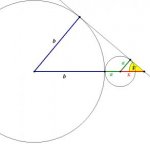
There is a small circle which is tangent to a large circle. The points P and R are outside of both circles. The line segment PR goes through the center of both circles. There is another point Q. The line segment PQ is tangent to both circles. The points P, Q and R form an angle which is outside of both circles with P at the vertex. Call the angle at point P: V. The radius of the small circle is a. The radius of the large circle is b.
Show that Sin V = (b-a)/(a+b)
What I have done:
I drew the diagram and labelled the points, angle and radii.
I drew the radius of the small circle, a, to the point where PQ touches the small circle. I called the distance form this point to the vertex of the angle g.
I drew the radius of the larger circle, b, to the point where PQ touches the circle. I called the distance from the point where a touches the small circle to b touches the larger circle h.
I found that Sin V = a/h and Sin V = b/(g+h)
Therefore, a=hSin V and b= (g+h)Sin V
b=gSin V + hSin V
Substituting b=gSin V + a
b-a= gSin V
Sin V= (b-a)/g
I am not able to prove g=a+b?
I think I have done somthing wrong in the expression for Sin V?
I am not sure the angle at the center of each circle is 90 degrees, but I am confused?
Thank you for any help you can give me.
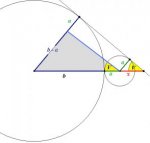
There is a small circle which is tangent to a large circle. The points P and R are outside of both circles. The line segment PR goes through the center of both circles. There is another point Q. The line segment PQ is tangent to both circles. The points P, Q and R form an angle which is outside of both circles with P at the vertex. Call the angle at point P: V. The radius of the small circle is a. The radius of the large circle is b.
Show that Sin V = (b-a)/(a+b)
What I have done:
I drew the diagram and labelled the points, angle and radii.
I drew the radius of the small circle, a, to the point where PQ touches the small circle. I called the distance form this point to the vertex of the angle g.
I drew the radius of the larger circle, b, to the point where PQ touches the circle. I called the distance from the point where a touches the small circle to b touches the larger circle h.
I found that Sin V = a/h and Sin V = b/(g+h)
Therefore, a=hSin V and b= (g+h)Sin V
b=gSin V + hSin V
Substituting b=gSin V + a
b-a= gSin V
Sin V= (b-a)/g
I am not able to prove g=a+b?
I think I have done somthing wrong in the expression for Sin V?
I am not sure the angle at the center of each circle is 90 degrees, but I am confused?
Thank you for any help you can give me.