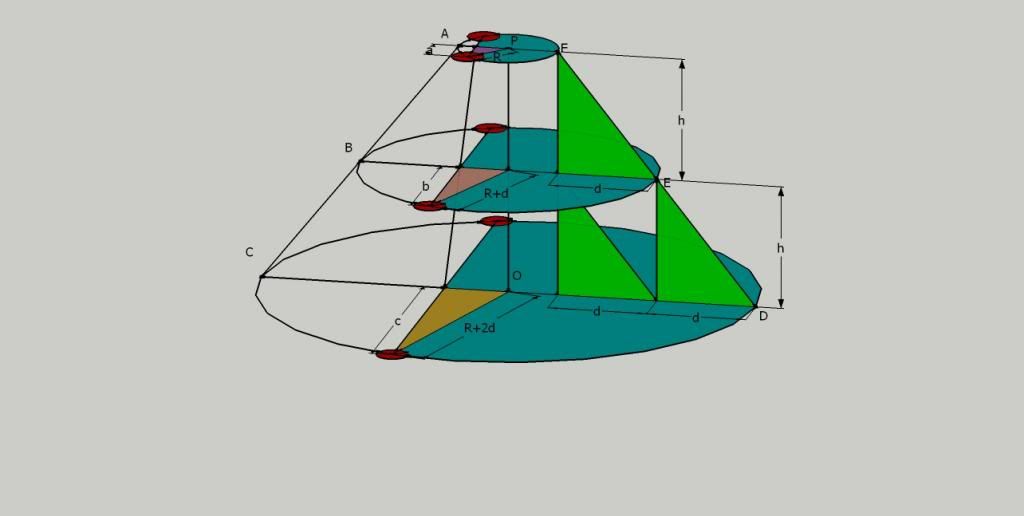
In the diagrams below there are 3 circles vertically seperated by distance 'h'. A straight line passes through the centre of each chord. ABC and DEF are straight lines, OP passes through the centre of each circle.
a, b, c and h are known.
The second diagram is to show that the circles can be moved in their respective planes whilst the knowns and unknowns remain the same.
I do know that if 'd' is increased and OP still passes through the centre of each circle them ABC and DEF are no longer straight lines.
Is it possible to obtain equations for R and d in terms of these known quantities?
Many thanks for any help.
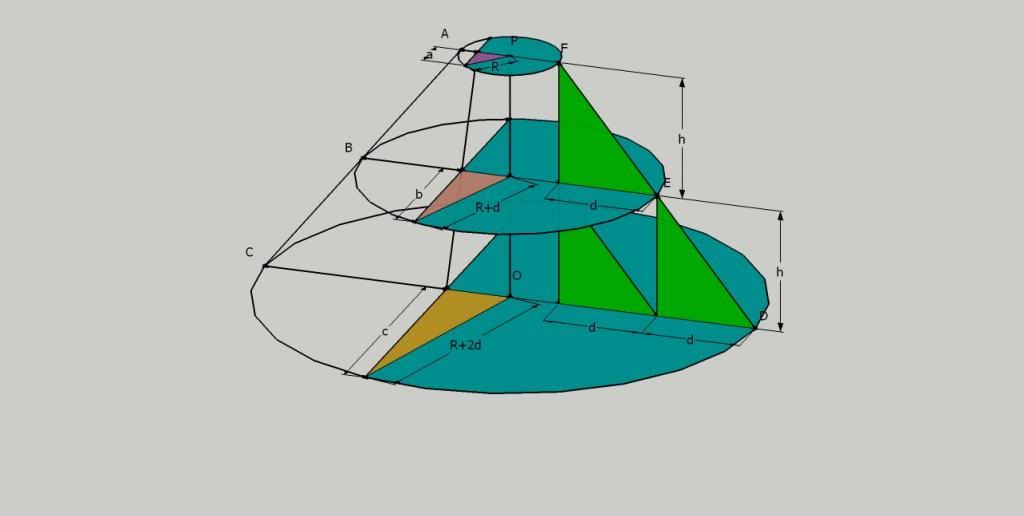
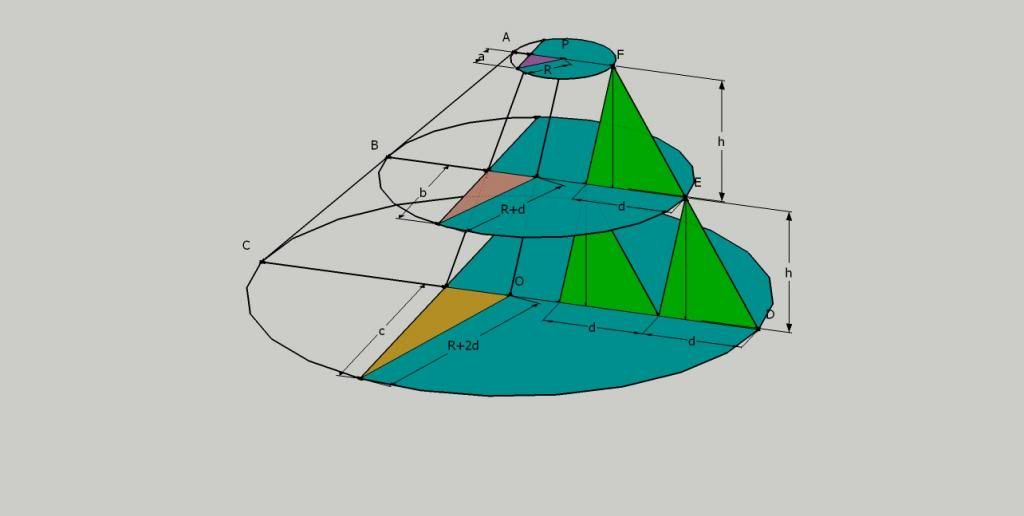
a, b, c and h are known.
The second diagram is to show that the circles can be moved in their respective planes whilst the knowns and unknowns remain the same.
I do know that if 'd' is increased and OP still passes through the centre of each circle them ABC and DEF are no longer straight lines.
Is it possible to obtain equations for R and d in terms of these known quantities?
Many thanks for any help.