Hello! I have been working on brushing up on my Algebra skills since it has been years since I have had to think about any of this stuff, and I've come across a problem that has thrown me for a loop.
I need to solve for k. Here is the problem.
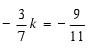
I have the answer key, and according to the key, the answer is that k = 21/11 (or 1 10/11.) Unfortunately I cannot figure out how to get to that answer.
The first thing I did was to add -3/7(k) and -9/11 to each side so I wouldn't have to be dealing with negatives.
-3/7 (k) = -9/11
9/11 = 3/7 (k)
The next thing I did was to try to create a common denominator by multiplying each side by the other for a denominator of 77.
63/77 = 33/77 (k)
And that's kind of where I'm stuck. I think I can divide 63 by 33 and end up with 1.909, which I assume is the same as 21/11... but my answer needs to be in the form of a fraction. Am I on the right track? What are the steps to solve for a variable when you are dealing with fractions like this? Normally I would just try to get the variable alone... but when I only have a fraction of the variable in the equation, I get really confused.
Thanks for your help!
I need to solve for k. Here is the problem.
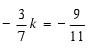
I have the answer key, and according to the key, the answer is that k = 21/11 (or 1 10/11.) Unfortunately I cannot figure out how to get to that answer.
The first thing I did was to add -3/7(k) and -9/11 to each side so I wouldn't have to be dealing with negatives.
-3/7 (k) = -9/11
9/11 = 3/7 (k)
The next thing I did was to try to create a common denominator by multiplying each side by the other for a denominator of 77.
63/77 = 33/77 (k)
And that's kind of where I'm stuck. I think I can divide 63 by 33 and end up with 1.909, which I assume is the same as 21/11... but my answer needs to be in the form of a fraction. Am I on the right track? What are the steps to solve for a variable when you are dealing with fractions like this? Normally I would just try to get the variable alone... but when I only have a fraction of the variable in the equation, I get really confused.
Thanks for your help!
