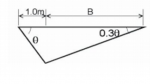
The question is - Determine the value of dimension B.
Just in case the values are hard to see, the angles are theta and 0.3 theta and the dimension is 1.0m.
From previous questions in the tutorial this is from, I assume the your answer can be in terms of theta and surely it needs to be. What I tried was splitting the triangle into two right angled triangles and finding the length of the common side in terms of theta using trig. Then used trig again on the right hand triangle to get B in terms of theta. This is the only thing i can think to do but I do not think it's right as there are 4 other questions like this, only the two numerical values are altered each time. If that was the answer it would be arbitrary to ask us to do the other questions.
Am I missing something?
Feel free to change theta to x or something if you're giving an answer
Thanks
