kinuel8091
New member
- Joined
- Jul 27, 2013
- Messages
- 24
A ship leaves the port at 12:00 noon heading west with a speed of square root of 3 knots. At 2:00 PM due to a navigational error, the ship turned at a bearing of N 60° W with at speed of 2 knots. How far is the ship from the port at 3:00 PM?
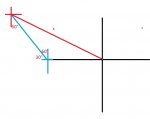
I 1st solved for the distance
d=rt
d=√3 *2
distance from start to the west 2√3
d=rt
d=2*1
d=2
distance from the west point from 2:00pm to the point of 3:00pm
Then what? i don't know what to do next
We only need to use the special angles. 60,30,45.
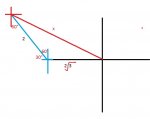
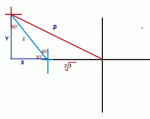
I 1st solved for the distance
d=rt
d=√3 *2
distance from start to the west 2√3
d=rt
d=2*1
d=2
distance from the west point from 2:00pm to the point of 3:00pm
Then what? i don't know what to do next
We only need to use the special angles. 60,30,45.