You are using an out of date browser. It may not display this or other websites correctly.
You should upgrade or use an alternative browser.
You should upgrade or use an alternative browser.
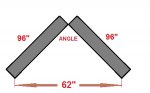
apex angle of 2 8 foot 4x4's that are 62 inches apart at the bottom.
- Thread starter jeep1965
- Start date
Apex angle?
Quaid Thank you for your reply! Your diagram is correct for the bottom but what I'm trying to figure out for the top is what degree the 4x4's need to be cut to lay flat together. Maybe "apex angle" isn't the correct terminology. Thank you for your help!
Quaid Thank you for your reply! Your diagram is correct for the bottom but what I'm trying to figure out for the top is what degree the 4x4's need to be cut to lay flat together. Maybe "apex angle" isn't the correct terminology. Thank you for your help!
HallsofIvy
Elite Member
- Joined
- Jan 27, 2012
- Messages
- 7,763
You can use the "cosine law": if a, b, and c are the lengths of sides of a triangle and C is the angle opposite side c, then \(\displaystyle c^2= a^2+ b^2- 2ab cos(C)\). Here, you can take a= b= 96 and c= 62 so this becomes \(\displaystyle 62^2= 96^2+ 96^2- 2(96)(96)cos(C)\) or \(\displaystyle 3844= 9216+ 9216- 18432 cos(C)\) which gives \(\displaystyle cos(C)= 0.79145\). The angle you need to cut is half of C.