paulweq123
New member
- Joined
- Mar 21, 2015
- Messages
- 6
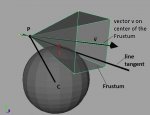
A line from P and touches the sphere in T , I want to find T.
I know P (x , y, z ) the center C ( 0,0,0) and ray R of the sphere.
View attachment 5138
A line from P and touches the sphere in T. .I want to find T.
I know P(x,y,z), the center C (0,0,0) and radius R of the sphere.
Unless I am misunderstanding the question, since (from a later post) line PC and PT lie in the same plane this problem is equivalent to the 'easier' problem:A line from P and touches the sphere in T , I want to find T.
I know P (x , y, z ) the center C ( 0,0,0) and ray R of the sphere.
my apologies im not sure if this is the place for this question.
Anyway thanks.
View attachment 5138
Thanks Ishuda, but in 3D these formula give me the point T?
the problem was not picked up a book , actually I need to solve this for visibility 3D game.I'm not sure if knowing the radius help on something, however these are known items of problem.The main question is :
Discover the T point or plane that just touch the surface of sphere at the point T.
The vector v would not help ?
or maybe there is no solution or missing something..
The difference is only that the points don't all lie in a z=constant plane, the lines PC & PT lie in the planeThanks Ishuda, but in 3D these formula give me the point T?
the problem was not picked up a book , actually I need to solve this for visibility 3D game.I'm not sure if knowing the radius help on something, however these are known items of problem.The main question is :
Discover the T point or plane that just touch the surface of sphere at the point T.
The vector v would not help ?
or maybe there is no solution or missing something..
Unless I am misunderstanding the question, since (from a later post) line PC and PT lie in the same plane this problem is equivalent to the 'easier' problem:
Given a circle of radius R centered at (0,0) and a point P=(x0, y0) what is the point T=(x1, y1) such that the tangent line at T passes through P? We actually have just changed tangent plane to tangent line and ignored the fact that the plane may have been translated, stretched, and/or rotated about all three axes.
So we have
x2+y2=R2
and
y' = -x/y
Thus P lies on the line
y = y1 - (x1/y1) (x-x1)
and
y0 = y1 - (x1/y1) (x0-x1) = \(\displaystyle \frac{y_1^2 - x_1 (x_0-x_1)}{y_1}\)
and, since \(\displaystyle y_1=\pm\sqrt{R^2-x_1^2}\), we have
\(\displaystyle y_0\, \sqrt{R^2-x_1^2} = \pm[R^2 - x_1^2 - x_1 (x_0-x_1)]\, =\, \pm[R^2 - x_0\, x_1]\)
which will result in a quadratic equation for x1 and thus (generally) have two solutions.
The difference is only that the points don't all lie in a z=constant plane, the lines PC & PT lie in the plane
(x0y1-x1y0) z + (z0y1-z1y0) x + (z1x0-z0x1) y = 0,
the line PT also lies in the tangent plane
z = z1 + fx(x1,y1) (x-x1) + fy(x1,y1) (y-y1)
and the point (x1,y1,z1) is on the sphere
x2 + y2 + z2 = R2
and
z = f(x,y) = \(\displaystyle \sqrt{R^2 - x^2 - y^2}\)
BTW: I would check the equation for the first plane up there, I could have made a mistake.
If you know the vector v, then you can write a different equation for the first plane equation I wrote which point T must satisfy. That may make the solution easier to compute but I'm not sure of that.thanks Ishuda!
So I can conclude that the ray R is essential for problem.There is no way to solve this problem inserting the vector v ?
For example, If I move the point P in some position around this sphere , the vector v(view direction) remaining always above the surface of the sphere , the point T must always be contained in the plane made by PC and the vector P+v .
That is, it is essential P+v lie on the same plane which PC and PT lie.
P is the position of airplane and v is a direction.
View attachment 5142
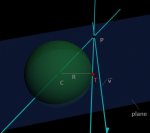
\(\displaystyle \mathbf v \cdot \mathbf w = \left\Vert{\mathbf v}\right\Vert \left\Vert{\mathbf w}\right \Vert \cos \theta\)I'm about finding a way to solve!
If I rotate the vector v around the normal N = (CP )x(v), for n degrees find a v1 vector, and scale by the distance equivalent to one of the catetos can find the point T.
The hardest part is to find the angle between v and v1!
View attachment 5148
