You are using an out of date browser. It may not display this or other websites correctly.
You should upgrade or use an alternative browser.
You should upgrade or use an alternative browser.
Arc of a Circle.
- Thread starter Thekoning
- Start date
I dont think it was confusing diagram.
Of course there is enough info given.
You guys were not very helpful with your posts.
I figured it out after re-discovering the Arc Length Formula (arcLength = (Ɵ/360)x2∏r)
Knowing that you can solve for "r" which is length "CB" and then find the rest using sin law stuff.

Of course there is enough info given.
You guys were not very helpful with your posts.
I figured it out after re-discovering the Arc Length Formula (arcLength = (Ɵ/360)x2∏r)
Knowing that you can solve for "r" which is length "CB" and then find the rest using sin law stuff.

.... Denis its okay if your still confused, you can start a thread to help clear up your confusions.
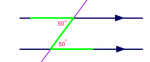
you can determine the central angle is 55 degrees using the "Z" pattern
 Make sense? There is a good quiz at the following links that i think will help you brush up on problems like these:
Make sense? There is a good quiz at the following links that i think will help you brush up on problems like these:
http://study.com/academy/practice/quiz-worksheet-alternate-interior-angles.html
Good luck Denice, it will come to you.
thanks for seeing d = 13.7 though, dont know how that happened
you can determine the central angle is 55 degrees using the "Z" pattern
 Make sense? There is a good quiz at the following links that i think will help you brush up on problems like these:
Make sense? There is a good quiz at the following links that i think will help you brush up on problems like these:http://study.com/academy/practice/quiz-worksheet-alternate-interior-angles.html
Good luck Denice, it will come to you.
thanks for seeing d = 13.7 though, dont know how that happened
- Joined
- Feb 4, 2004
- Messages
- 16,582
Denis is not confused regarding the material; he is quite proficient. He is confused about your statement of your particular exercise. For instance, as he pointed out, you had apparently withheld necessary information..... Denis its okay if your still confused...
To clear things up, please read the "Read Before Posting" that you were supposed to have read before posting, and then reply with a full and exact statement of the exercise, the complete instructions, and a clear listing of all of your efforts thus far. Once we can figure out what you're actually asking, the confusion should quickly dissipate.
Thank you!
The way I'm reading the diagram and statement of the problem as this is all the information which is available:Excuse me if im posting in the wrong section.
This is a question which has raised my interest.
Im trying to find length CB, and AD aswell as BD. Using the curved length of 16 feet, and the degrees 35(ABD).

Thanks
(1) Points A and B are on the circle
(2) Point D is (possibly) off the circle but would have the same y-ordinate as point A.
(2) Although you show the angle between the tangent line at point B and the line BD is 35 degrees what you mean is that the angle ABD (not shown) is 35 degrees.
Construction: Choose line AD parallel to the x axis. Pick an arbitrary point B. Point D is directly below point B and point A is on the line L1 at 35 degrees measured clockwise from line BD. Choose an arbitrary radius r. The center of our circle will lie on the circle CI1 centered at point B with radius r. Point A will be a distance d from B where
d = 2r sin(\(\displaystyle \frac{\theta}{2}) = 2r\, sin(\frac{8}{r})\)
Draw the circle CI2 centered at point B with radius d. The intersection of L1 and CI2 determine point A [there will be two such points so to be definite choose point to the left of B as in the diagram]. Now draw a circle CI3 with center at point A of radius r. The intersection of CI1 and CI3 determine the center of our circle. Since the radius r was (almost) arbitrary, the center of the circle, the length CB, the central angle BCA are all (almost) arbitrary.
