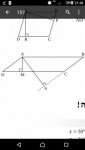
In the bottom Parallelogram it is given that AD=20 and that the perimeter is 140.
(Ok so therefore AB=DC=50).
It is also given that AS=AM+18.
We need to find AM, therefore AS and then to calculate the area of the Parallelogram which derives from finding AM.
Now, I managed to find the right answer but not the way to prove it, I just played around with Pythagoras.
If I could prove that SC=CB then the rest follows and AM=12, but I don't know how.
Please help, thanks!
