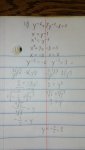(Quadratic type equation) - Missing four solutions to y^-6 + 7y^-3 -8 = 0

[codyw1996]

The problem is y^-6 + 7y^-3 -8 = 0.
I found two of the six solutions y = -1/2, 1.



However there are four other solutions (1 ± i√3)/2, and (-1 ± i√3)/2
I don't know how to find the last four.

 

[mmm4444bot]

The problem is y^-6 + 7y^-3 -8 = 0.
I found two of the six solutions y = -1/2, 1.

View attachment 7803

However there are four other solutions (1 ± i√3)/2, and (-1 ± i√3)/2 That pair is not correct
I don't know how to find the last four.

One approach involves polynomial division.

If we multiply each side of the given equation by y^6, we get

8y^6 - 7y^3 - 1 = 0

You already found two solutions: y = 1 or y = -1/2

Therefore, (y-1) and (2y+1) are factors of 8y^6 - 7y^3 - 1.

(y - 1)(2y + 1) = 2y^2 - y - 1

Can you divide (8y^6 - 7y^3 - 1)/(2y^2 - y - 1) longhand, using polynomial division?

The quotient is a fourth-degree polynomial that factors (by guess-and-check) as the product of two quadratic polynomials. :cool:

 

[codyw1996]

Sorry, that was a typo. I meant to type (1 ± i√3)/4

And I figured it out. If you set both y^3 = -1/8 and y^3 = 1 to zero ( y^3 + 1/8 =0 and y^3 -1 =0) you can factor them to find more solutions.

 

[mmm4444bot]

I meant to type (1 ± i√3)/4 Good!

If you set both y^3 = -1/8 and y^3 = 1 to zero ( y^3 + 1/8 =0 and y^3 -1 =0) you can factor them to find more solutions.

Yes, that is another method.

 

[mmm4444bot]

How

Their work shows how.

They substituted x = y^(-3), and solved the resulting quadratic equation in x.