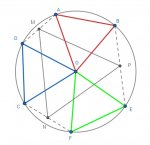
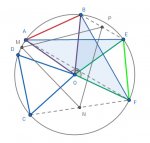
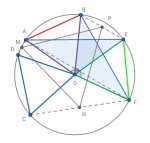
Equilateral triangles (marked); M, N, P are midpoints of AD, CF, EB. Prove MNP is...

[Taric]

The red triangle, the green one and the blue one are equilaterals.
M, N and P are the midpoints of AD, CF and EB.
Prove that MNP is equilateral.

 

[Deleted member 4993]

The red triangle, the green one and the blue one are equilaterals.
M, N and P are the midpoints of AD, CF and EB.
Prove that MNP is equilateral.

What are your thoughts regarding the assignment?

Please share your work with us ...even if you know it is wrong.

If you are stuck at the beginning tell us and we'll start with the definitions.

You need to read the rules of this forum. Please read the post titled "Read before Posting" at the following URL:

http://www.freemathhelp.com/for

 

[Taric]

I've found that AOE and BOF are similar triangles. Hence AE = BF and BEFA is an isoscele trapezoid.

 

[Taric]

Trapezoid

AOE and BOF are similar triangles. Hence ABEF is an isosceles trapezoid. And that's all I could find

 

[Taric]

What else can you say about these 3 triangles?

There is nothing relevant to say about them

 

[Taric]

They are also congruent.

Yes, they are

 

[yma16]

proof

The red triangle, the green one and the blue one are equilaterals.
M, N and P are the midpoints of AD, CF and EB.
Prove that MNP is equilateral.

 

[Taric]

Very impressive!

View attachment 9651View attachment 9652

Thanks a lot for this solution.
Meantime, I've found another one, using complex numbers (I mean affixes)